Emily Pope, St. Francis Xavier University
Jennifer Mitton, St. Francis Xavier University
Correspondence concerning this article should be addressed to Emily Pope epope@lakeheadu.ca
This paper focuses on how Inuit students responded to a Southern mathematics teaching strategy, known as number talks, in a Nunavut elementary school. Research on the effectiveness of number talks has been conducted in the elementary context (Boaler, 2015; Murata et al., 2017), yet there is little research that focuses on Inuit students’ perspectives of number talks as part of mathematics learning. The participants of the study included 10 students and their teacher in a Grade 1 classroom. Data methods included participant interviews, classroom observations, and artefacts generated in response to number talk routines. The results of this affirm what is known about the benefits of number talks and afford new understanding about how to view the teaching strategy through Inuit Qaujimajatuqangit (IQ) principles as outlined by the Nunavut Department of Education (2007).
Keywords: Inuit, number talks, culturally relevant pedagogy, elementary school, Inuit Qaujimajatuqangit (IQ) principles
Exploring Inuit Students’ Responses to Number Talks
Teaching practices from the South are an interwoven part of Nunavut’s Education system. Despite the government’s efforts to create a more culturally responsive education system (Berger, 2009), a Eurocentric education model constrains schooling in Nunavut. Scholars have noted that the majority of Inuit in Nunavut want to see their culture reflected in the education system, they want Inuktitut to be strengthened, and they have high academic standards for their children (Aylward, 2007, 2009, 2010; Berger, 2009; McCarty & Lee, 2014). Researchers have noted that what has been largely missing in the pedagogy of teachers from the South is the incorporation of culturally responsive teaching strategies (Gay, 2013; Ladson-Billings, 1995; 2014) to support Inuit learners in the Nunavut classroom (Aylward, 2007, 2009, 2010; Berger, 2009; Preston, 2016).
In Nunavut, the Inuit Qaujimajatuqangit (IQ) principles outlined by the Nunavut Department of Education (2007) represent the Inuit societal values that are valued in the Inuit culture. The IQ principles are meant to ground Nunavut education in the Inuit heritage with the aim that students will be successful in modern Nunavut (Consolidation of Education Act, 2020). In Nunavut, educators are expected to incorporate the IQ principles into their daily teaching (Consolidation of Education Act, 2020; Nunavut Department of Education, 2007). Not all teaching practices that are created outside of Nunavut, however, are able to incorporate or align with the IQ principles. In this context, we saw the possibilities of exploring an elementary teaching strategy known as number talks (Parrish, 2014). Number talks are used to encourage students to share and defend their solutions to mathematics problems and the strategies they used, which allows learners to “collectively reason about numbers while building connections to key conceptual ideas in mathematics” (Parrish, 2014, p. 5). The purpose of this study was to explore how Inuit students responded to the use of number talks, and the strategy’s alignment with the IQ principles.
Number talks have been found to be successful at teaching both number sense and mathematics facts (Hufferd-Ackles et al., 2004). Integral to the routine of number talks and understanding student learning is number sense. Number sense is the ability to understand the mathematical relationship between numbers and is not simply the memorization of mathematical facts or equations (Boaler, 2015), which is why number sense is used in the mathematics education reform approach “as it typifies the theme of learning mathematics as a sense-making activity” (McIntosh et al., 1992, p. 3). Number sense is an important concept in the teaching and learning of number talks, as it provides windows into the depth of student learning. Being able to understand and show the mathematical relationship between numbers through communication (Boaler, 2015) was critical to this study as we explored Inuit students’ responses to number talks.
The success of number talks in some schooling contexts is why Stott and Graven (2015) chose to investigate how number talks could be used in South African schools with the aim of increasing students’ mathematical capabilities. Murata et al. (2017) identified that certain teacher talk moves support the development of students’ understanding of how to discern the best strategy to use while allowing them to maintain ownership of ideas. For example, asking a student “how did you get to that answer” prompts students to explain their reasoning and reflect upon their approach. Research on the effectiveness of number talks has been conducted in elementary schools (Boaler, 2015; Murata et al., 2017), yet there is little research that focuses on Inuit students’ perspectives of number talks as part of mathematics learning in an elementary context. While there has been research around mathematics education with Inuit outside of Nunavut (Bergquist, 2020; Poirier, 2007), our study aimed to address the lack of research about mathematics education in Nunavut.
A teacher’s pedagogy plays an important role in the mathematics classroom when it comes to setting up the conditions for student success. The findings from Murata et al. (2017) highlighted the important role teachers play in the implementation of number talks, as this strategy requires teachers to shift away from traditional teaching methods (Parrish, 2014). For number talks, Parrish (2014) explained that teachers need to assume “the interrelated roles of facilitator, questioner, listener, and learner” (p. 12) to best support student learning. Depending on a teacher’s ability to assume those interrelated roles, the nature of a teacher’s interactions with students while facilitating number talks suggests a relationship between student learning and the level of mathematical understanding (Murata et al., 2017).
The primary purpose of this study was to explore how Inuit students experienced and responded to learning mathematics using daily number talks. Because of the importance of teacher pedagogy to number talks, a secondary focus included exploration of a teacher’s pedagogical practices through classroom observations. The primary research question was: What are Inuit students’ perspectives on learning mathematics using daily number talks? While neither author speaks Inuktitut, the primary language spoken in Nunavut, the hope is that this research may resonate with teachers who teach mathematics in elementary classrooms and with students from groups that have been historically marginalized.
Berger (2009) found that the Nunavut education system is “[…] based primarily on the knowledge, pedagogy and culture of Euro-Canadians […]” (p. 56) rather than on culturally relevant practices that take into account the Inuit culture (Aylward, 2007; Ladson-Billings, 1995). Lipka (1994) described a similar situation in Alaskan education, stating “this lack of responsiveness by the educational establishment continues to underscore the colonial nature of schooling which too often undermines indigenous language and culture” (p. 14). Berger (2009) maintained that there is still a Eurocentric education model in Nunavut, despite the government’s efforts to create a more culturally responsive education system. These efforts included the publishing of Inuuqatigiit: The Curriculum from the Inuit Perspective (Northwest Territories Education, Culture and Employment, 1996) and the training and hiring of Inuit educators to teach in Nunavut schools. Berger (2009) argued that “Eurocentrism may act as a roadblock to educational change in Nunavut” (p. 57) because the voices and opinions of non-Inuit are often valued and honoured over Inuit perspectives. In this study, we have attempted to honour the perspectives of Inuit students by maintaining our attention upon their responses to number talks and through interviewing a small sample of students.
The teaching of Inuktitut so that students can be truly bilingual (Aylward, 2009; Indian and Northern Affairs Canada, 2002; McCarty & Lee, 2014) is an important goal in Nunavut. However, Aylward (2009) found upon examining teachers’ beliefs around the presence of Inuit languages within Nunavut schools that teachers in Nunavut were disappointed with the lack of a culturally relevant curriculum. Teachers also highlighted that importing curriculum from other provinces and territories did not benefit their students (Aylward, 2010). Over time, Aylward (2007, 2009), and others (Berger, 2009; Government, 2021; Preston, 2016), have argued for increased accountability within the Nunavut education system regarding bilingual education and students’ abilities to understand Inuktitut and the importance of including families and communities. Parental and community engagement within the school system is an important way of encouraging Inuktitut (Aylward, 2009, 2010) and culturally relevant teaching practices within Indigenous schooling contexts (McCarty & Lee, 2014). Such curricular efforts have shown promise in other Indigenous contexts. For example, Lipka et al. (2005) have shown how a culturally based mathematics curriculum, Math in a Cultural Context (MCC), has been beneficial to their mostly Yup’ik students in Alaska. This is because the curriculum allowed the students to engage in complex mathematics based on practical problems from their village, such as building a fish rack (Lipka et al., 2005). Lipka et al. (2005) found evidence that the MCC curriculum has resulted in improvement in Indigenous Alaskan students’ academic performance. Their research has also shown that the MCC curriculum supports a guided inquiry approach which promotes cooperative learning and classroom norms that encourage class discussion (Lipka et al., 2005).
For many scholars, learning mathematics is viewed as a sociocultural process (Esmonde, 2009; Forman et al., 1997). Sfard (2007) described discourse as a communicational activity in which some individuals can participate while others are excluded. Gee (2005) described discourse as how “we continually and actively build and rebuild our worlds not just through language but through language used in tandem with actions, interactions, non-linguistic symbol systems, objects, tools, technologies, and distinctive ways of thinking, valuing, feeling, and believing” (p. 10). Both these descriptions of discourse emphasize that to engage in a communicational activity, individuals need to participate in the building or rebuilding of a perceived reality using a common language, including oral language, gestures and symbols. By participating in mathematical discourse, scholars have argued that students promote their conceptual understanding of mathematics while strengthening their ability to communicate their thinking to peers instead of solely focusing on finding answers (Boaler, 2015; Cavanna et al., 2015; Esmonde, 2009; Forman et al., 1997; Henning et al., 2012; Hufferd-Ackles et al., 2004; Parrish, 2014). Although there is evidence to show the importance of mathematics activities that focus on communication as a way to develop learning, there are multiple approaches to the teaching of mathematics ranging from a traditional approach to a reform approach (Boaler, 2002; Herbel-Eisenmann et al., 2006; Morgan & Sfard, 2016).
In a traditional classroom, one can characterize classroom instruction as the transmission of facts and information from the teacher to the students (Forman et al., 1997). Most often, this is through paper and pencil activities, which has been the predominant way of teaching in Nunavik according to Poirier (2007). In contrast, the reform teacher adopts a constructivist or conceptual approach to teaching mathematics which is based on posing open-ended problems in order to encourage students to develop their own way of solving the problem and to engage them in mathematical discussions with their peers as a way of learning (Boaler, 2002). Instead of rote learning, researchers have argued that students’ number sense develops more fully through the use of daily number talks or math talks, as these kinds of approaches help students to develop flexible and accurate computation strategies that are based on key mathematical ideas (Boaler, 2015; Parrish, 2011, 2014).
According to Hufferd-Ackles et al. (2004), a math-talk learning community is one in which students and teachers use mathematical discussions to support mathematical understanding. Through participation in the discourse of mathematics, students are able to expand their own thinking as well as the thinking of others (Hufferd-Ackles et al., 2004). Murata et al. (2017) explained that by talking and listening to others talk about mathematical concepts, students think more deeply about the concepts while engaging in mathematical practices that include argumentation and justification.
The Benefits of Implementing Number Talks: An Example. Stott and Graven (2015) worked within the South African Numeracy Chair project looking at mathematics education in South Africa and investigating how number talks could be used in their South African schools. Given the different school and cultural contexts, Stott and Graven (2015) knew that some adaptations to number talks, as outlined by Parrish (2014) and Boaler (2015), were needed to meet the needs of South African students most effectively. For example, in the United States number talks are used with class sizes that are much smaller than in South African schools (Stott & Graven, 2015). Some of the adaptations included allowing the students to work in small groups before discussing the problem as a whole class and getting the teacher to record student responses on the board. Through these adaptations and the creation of teacher resources, teachers found that their students’ mathematical conceptual development was strengthened through the use of number talks (Stott & Graven, 2015). While number talks have been used in settings outside of North America with different cultures (Stott & Graven, 2015), there has been little to no research that explores Inuit student perspectives of number talks. In what follows, we discuss the theories that supported our understanding of student responses to number talks.
Given the focus on Inuit students’ responses to number talks, the theoretical framework informing this study is comprised of several concepts related to culturally relevant pedagogy (Ladson-Billings, 1995, 2014) as well as sociocultural theory (Vygotsky, 1995), and the IQ principles of the Nunavut Department of Education (2007). Ladson-Billings’ (1995) seminal work on culturally relevant pedagogy, and its various evolutions in contributions from scholars such as Paris (2012) and Paris and Alim (2014), focused on ensuring students from all cultures succeed at school while maintaining their home culture. McCarty and Lee’s (2014) term of culturally sustaining/revitalizing pedagogy go a step further to focus specifically on Indigenous Peoples. This, in conjunction with Vygotsky’s (1978) sociocultural theory and the IQ principles that represent the Inuit societal values (Nunavut Department of Education, 2007), forms the basis of the theoretical framework of this study.
Castagno and Brayboy (2008), Munroe et al. (2013), and Russell and Chernoff (2013) all agreed that when it comes to teaching Indigenous students, their cultures and language need to be incorporated into a teacher’s pedagogy in order to make learning accessible, relevant, sustaining, and revitalizing. McCarty and Lee (2014) defined culturally sustaining/revitalizing pedagogy as having three components. These three components include addressing colonization and Eurocentric viewpoints, reclaiming and revitalizing the languages lost through colonization, and ensuring community-based accountability (McCarty & Lee, 2014).
Vygotsky believed that cognitive development is grounded in its social context and that learning occurs as a part of the internalization of social and cultural values in a given social context (Inan & Yuksel, 2013). Sociocultural theory, according to Vygotsky, incorporates both developmental and sociocultural elements to explain how individuals learn (Inan & Yuksel, 2013). Furthermore, Vygotsky’s research supports the idea that oral communication can help facilitate students’ development in the mathematics classroom, as he believed that by using language to explain their thinking, children are able to internalize learning (Vygotsky, 1978). It is a child’s social interactions with their peers and teachers that allow them to internalize the activity and therefore understand the concept (Stott & Graven, 2015). Learning should be a social activity that develops out of a collaborative and cooperative learning environment (Inan & Yuksel, 2013).
In Nunavut, the IQ principles represent Inuit societal values that are respected in the Inuit culture (Nunavut Department of Education, 2007). The IQ principles, if implemented, would ground Nunavut education in Inuit heritage so students would be successful in modern Nunavut. In Nunavut, educators are expected to incorporate the IQ principles into their daily teaching (Nunavut Department of Education, 2007). The IQ principles enable non-Inuit researchers and educators to more fully understand the societal values of students, their families, and their community as a way to best meet their learning needs. The IQ principles as outlined by the Nunavut Department of Education (2007) highlight the ways in which individuals collectively engage in the act of learning with each other. For example, Inuuqatigiitsiarniq refers to our relationship with others; Tunnganarniq refers to being welcoming and inclusive; Pijitsirniq refers to serving others and the community; Aajiiqatigiinniq refers to making decisions through discussion; Pilimmaksarniq refers to the act of learning through various means such as observation and practice; Piliriqatigiinniq refers to collaboration in order to achieve a common goal; Qanuqtuurniq refers to being resourceful when it comes to problem-solving; and Avatittinnik Kamatsiarniq refers to environmental stewardship.
In this research study, maintaining a focus on student participants and their teacher required a framework that enabled us to consider student interactions with each other and their teacher as they engaged in thinking aloud during number talk engagement in this elementary classroom. As part of the analysis of classroom observations and interviews, we were mindful that many of the IQ principles are reflected in the conduct of number talks, specifically Inuuqatigiitsiarniq, as the act of sharing their thinking with a peer is an integral part of number talks, and Piliriqatigiinniq, or the collaboration that evolves during the whole class discussion. Ideally the act of engaging in number talks is also respectful of the principle, Tunnganarniq, as all students are able to participate and feel some measure of success. Perhaps most aligned with number talks are the IQ principles of Pilimmaksarniq (learning through observation and practice) and Qanuqtuurniq (being resourceful while problem-solving) as number talks encourage students to find ways to solve the problem that works for them. Cultivating an environment in which students feel safe and secure to take academic risks (Mitton & Murray-Orr, 2021; Matney et al., 2020) is also an important part of number talk instruction and engagement and is reflected in the IQ principles of Inuuqatigiitsiarniq and Tunnganarniq, which respectively emphasize relationship with others and being warm and inclusive. Drawing upon Vygotsky’s (1978) sociocultural theory in connection with the IQ principles enabled us to better understand the ways in which student participants communicated while engaging in number talks as their communication provided insights into their learning. Informed by this framework, attending to field notes on classroom observations and student accounts of their learning during interviews enabled us to identify how students responded to number talks and to see if number talks encouraged them to regularly engage in dialogue as a way to reveal their inner thinking during the learning of mathematics.
According to Merriam and Tisdell (2016), for an individual to be able to understand a given phenomenon, they must consider their own understanding about the phenomenon within a social context. Earlier conceptualizations of common approaches to qualitative research, Merriam and Tisdell explained, refer to such undertakings as “generic, basic, and interpretative” (p. 23) with an emphasis placed on understanding how people make sense of their lives through revealing and rendering these meanings. Drawing upon Merriam and Tisdell (2016), Lahman (2024) suggests that while the category of basic qualitative research is useful, it “does not capture the careful planning and extensive time and resources that go into conducting essential qualitative research” (p. 101). Instead, Lahman (2024) asserts, that common approaches to qualitative research should be referred to as “essential” as the descriptor “indicates research with the requisite features of qualitative research while not belonging to a specific methodology… [as it] primarily relies on data collected from interviews but may draw on some observation or focus on material data” (p. 101). Given that the focus of this study was upon understanding how Inuit students interpreted their number talk experiences in an elementary mathematics classroom through student interviews and classroom observations, our decision to use an essential qualitative research approach (Lahman, 2021, 2024) was well-suited to the intent of this study. Further informing this study are what Lahman (2024) has defined as the tenets of “culturally responsive research” (p. 18), which she explains include “a commitment to drawing on the cultural knowledge, prior experience frames of reference, and research communication styles of diverse research participants (differentiated by race/ethnicity, sexual orientation, class, disability, gender, age, etc.) to make research encounters more relevant and beneficial for them” (p. 19).
As the strategy of number talks was being implemented in this Nunavut elementary school, we were curious about how Inuit students might make sense of this approach in the learning of mathematics, and if it showed potential to be well aligned with Inuit ways of learning as reflected within many of the IQ principles (Nunavut Department of Education, 2007). We are mindful that while the study was situated within the Inuit territory of Nunavut, the education system continues to feel and reflect colonization (Aylward, 2007, 2009; Preston, 2016; Rasmussen, 2011), with most of its teachers neither Inuit nor from the North (Government of Nunavut, 2021; Preston, 2016). Perhaps, naively, we were hopeful that we would see some potential for number talks to be a culturally responsive teaching tool that might benefit Inuit students and unearth the meaning that students attributed to number talks while learning mathematics. An essential qualitative study, nested within the tenets of culturally responsive research (Lahman, 2024), enabled us to be mindful of the phenomenon under investigation, as students were encouraged to share their perspectives on how they learned mathematics best, while we considered the possibilities of number talks, a teaching and learning strategy imported from the South.
The study took place in a K-5 elementary school in Iqaluit, the capital of Nunavut, during the 2019-2020 school year. Ten students and one teacher situated in a Grade 1 class participated in the study. Most of the Grade 1 students were Inuit, and the others were of other cultural and racial backgrounds. Because we do not want the identities of those who participated compromised, we have chosen to not include detailed descriptions of student backgrounds. The school focused on the incorporation of the IQ principles as part of its regular programming and the medium of instruction was English. For example, Inuit Elders taught students how to sew once a week and engaged them in other Inuit knowledge activities. Monthly assemblies incorporated the IQ principles for both staff and students to learn more about the principles and how they apply to teaching and learning. As part of this focus, land-based activities engaging students and teachers took place throughout the year at the elementary school.
The teacher and students were observed during number talks as part of mathematics instruction, twice a week over a seven-week period, for a total of eight observations. As the focus of this study was on better understanding how students responded to number talks, regular classroom observations enabled us to view student interactions with each other and with their teacher. Additionally, because we were curious about student perceptions of number talks, two Inuit students, Elizabeth and Thomas1, were interviewed at the start and end of the study. The classroom teacher, Mrs. Piper, agreed to take part in the study as part of classroom observations but was not interviewed. Mrs. Piper, at the time of the study, had been teaching for 11 years with five years of experience at the Grade 1 level. Although Mrs. Piper is not originally from Nunavut (she is of European settler origin) and does not speak Inuktitut, she had chosen to create a life in Nunavut and was committed to the community and her students. As the strategy of number talks was being implemented in the school, Mrs. Piper was interested in taking part in the study. Part of her decision was also based on her participation in a professional learning community that focused on the exploration of number talks. Prior to these experiences, Mrs. Piper had not routinely used number talks as part of her mathematics teaching, introducing the strategy to her students in January 2020.
Oral communication was encouraged in Mrs. Piper’s class, even before the formalized introduction of number talks. Students were used to working at centers in peer groups and learning together as a whole class. When student participants were asked about where they engaged in mathematics in the classroom, they indicated that mathematics took place at their tables. When working at their tables, students were able to rotate through the centers which they had completed either independently or with assistance from their peer group. Students were encouraged to ask each other for help during learning activities, a strategy which respects the principle of Piliriqatigiinniq or working together for a common cause.
As a teacher in Nunavut, Mrs. Piper was very familiar with the IQ principles and was encouraged to incorporate those principles into her daily teaching (Nunavut Department of Education, 2007). In this school, over the course of the academic year, the IQ principles are regularly discussed among teachers and students. Students in Mrs. Piper’s class were in their second year at the school and most likely had already been introduced to the IQ principles and had engaged in learning activities and conversations about the IQ principles. Thomas and Elizabeth’s comments regarding peer group discussions as a part of mathematics learning suggested they were familiar with the incorporation of the IQ principles Aajiiqatigiinniq (decision-making through discussion and consensus) and Pilimmaksarniq (development of skills through mentoring, practice, observation and effort) in their classroom.
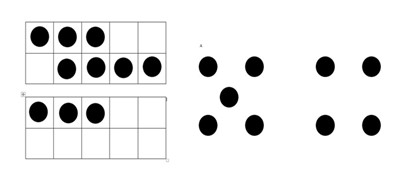
The number talks took place after lunch at the start of a dedicated mathematics period. To structure the number talks, Mrs. Piper used three different questions from Parrish’s (2014) book. The questions were visual representations of dots in either a ten frame or loose, were recreated on the computer, and printed on legal-sized paper. While dots are a common way to structure number talks, they do not necessarily hold cultural relevance for students in Nunavut. Out of the eight number talks observed, seven involved dots that were represented in ten frames or loosely on the page while one number talk involved addition sentences. The decision to focus on visual representations of dots was made in consultation with Mrs. Piper, as both the teacher and Emily (first author) felt that starting with something the students were familiar with might allow for more discussion. Mrs. Piper generally asked the students to tell her how many dots there were all together at the start of each question. In other words, the only new aspect of their mathematics classroom would be the number talk routine and not the mathematics involved.
Emily Pope is a cisgender, able-bodied white female of European heritage born and raised in Canada’s south. Before beginning the study, she had lived in Nunavut for 5 years in two different communities as a teacher and had worked in a third community for shorter periods of time throughout her undergraduate degree. Through her role as a teacher in Nunavut, Emily actively participated in school and community cultural events so that she could best incorporate Inuit societal values and IQ principles into her classroom. At her first school, she worked closely with the Ilinniarvimmi Inuusiliriji, or the School Community Counsellor, to better understand her students’ cultural backgrounds. At the time of the study, Emily was living in the community and teaching at the school where the research took place. She worked closely with colleagues to create monthly assemblies in which the IQ principles were highlighted to students. Jennifer Mitton (second author) is a professor of secondary literacy and qualitative research methodologies at a university situated in the Canadian Maritimes. Jennifer’s teaching and research focuses on culturally relevant pedagogy and the ways teachers foster academic risk-taking while working with culturally and economically diverse groups. The study was undertaken to partially fulfill the requirements of Emily’s Master of Education degree, with Jennifer working alongside Emily as her thesis advisor.
Following ethics approval and permission from the St. Francis Xavier University Research Ethics Board, the Nunavut Research Institute, and the Nunavut Department of Education respectively, Emily hosted an information session about the research study at the school for children and families. During this session, the study was presented, and questions were answered about the focus of the study and student involvement. Parents signed a consent form allowing their child to participate and this was followed by a conversation with each child, using appropriate language, to also confirm their assent to participate in the study.
The study took place over seven weeks in 2020 prior to the Covid-19 pandemic. Semi-structured interviews, classroom observations, and number talk artifacts (Merriam & Tisdell, 2016) were used as data collection methods. Through eight classroom observations and two interviews with two Grade 1 students, as researchers, we investigated how students responded to the use of number talks in a Nunavut school. Mrs. Piper introduced number talks to her students in January 2020 and classroom observation began with this introduction. Number talks typically ranged in length from 10-20 minutes each and took place at the beginning of the mathematics period.
The first interview with Elizabeth and Thomas took place before the implementation of number talks and the second interview took place following the final classroom observation. Each interview lasted between 10 and 15 minutes and Emily conducted the interviews. The first interview provided a baseline understanding of how Elizabeth and Thomas viewed learning mathematics while talking and what they thought about sharing their ideas with others. The second interview gave us insights into participants’ thoughts about the overall process of number talks and whether their ideas aligned with Emily’s observations. During the second interview, Elizabeth and Thomas were asked again about how they felt about learning mathematics during the whole class discussion and if they experienced any benefit from hearing others’ solutions to problems.
Classroom Observations and Artifacts
To explore how the ten student participants responded to number talks, eight classroom observations were conducted twice per week between weeks two to five. Fieldnotes were taken during observations which described the pedagogical practices Mrs. Piper used during number talks and documented student responses to number talks, including interactions with each other and the teacher. As Emily was a teacher in the school at the time of the study, this seven-week data collection timeline made it feasible for her to engage in the study while teaching full-time. As part of the observations, photographs of classroom layout, organization, student seating, and chart paper reflecting thinking during number talks were gathered; these artifacts (60 in total) enabled us to better understand how students responded to number talks in the classroom. During classroom observation, Emily documented whether student dialogue encouraged or discouraged additional talk moves. For example, was the purpose of the talk to find an answer or was it to explain their thinking? Identifying whether students engaged in mathematical argumentation, justification, or conceptual explanations during number talks were also documented.
Data analysis was guided by maintaining a focus on how Grade 1 Inuit students responded to daily number talks in a Nunavut elementary classroom. This analysis process began during data collection while field notes of classroom observations were documented, photographs of number talk artifacts were captured, and interviews were conducted. Engaging in data analysis in ongoing and recursive ways supported our aim to pinpoint common patterns across data sources (Merriam & Tisdell, 2016). What was learned through the analysis of one day’s worth of data collection in this study impacted the next day’s data collection and analysis. Ongoing analysis began with open codes to identify concepts, keywords, or phrases about the phenomenon that emerged (Merriam & Tisdell, 2016). For example, during this phase we were mindful of the research literature and what is known about student responses to number talks in addition to the theoretical framework; some codes such as opportunities for communication of ideas (Boaler et al., 2015, Cavanna et al., 2015) and the presence of routine (Michaels & O’Connor, 2015; Parrish, 2014) were expected. Other open codes that emerged from the data were quality of discussion, the presence of tabletop activities and manipulatives, permission to fail, and one-to-one conversations.
As the data analysis progressed, we moved from attending to what was emerging (inductive analysis) to pinpointing if patterns were present across data sources (deductive analysis). At a later phase of analysis, open initial codes were grouped into tentative categories, creating axial codes (Meriam & Tisdell, 2016). These categories were aligned with the IQ principles and the belief that oral communication, drawing upon Vygotsky’s (1978) sociocultural theory, is important for developing understanding. This process also included identifying any resonance with culturally relevant pedagogy. Axial codes, also known as analytic codes, “span many individual examples (or bits or units of the data…previously identified) of the category” (Merriam & Tisdell, 2016, p. 206). For example, open codes such as the presence of routine, communication of ideas, and teacher’s actions in structuring number talks were grouped into a category we refer to as “student responses to routinizing number talks”. The development of categories was an important step in the data analysis process as they revealed the ways in which students responded to number talks.
Our findings suggest that the students in this study responded positively to number talks based on their willingness to engage in dialogue about their thinking. In our analysis, we noted the importance of a routine, student familiarity with dot patterns, and Mrs. Piper’s pedagogy to their engagement in number talks. Each of these components was important to how students made visible their understanding of number sense. Number talks provided culturally relevant learning opportunities for students, offering them chances to verbalize their thinking in how they asked questions, made choices, and assessed their decisions in conversations with others. Such acts, for example, align with the IQ principles of Aajiiqatigiinniq (making decisions through discussion), Pilimmaksarniq (using different means to learn), Piliriqatigiinniq (collaborating to achieve a goal), and Qanuqtuurniq (resourceful problem solving).
The use of a routine encouraged students to participate in number talks. Student willingness to engage in dialogue happened over time as they grew more comfortable with the activity. Mrs. Piper worked hard at establishing this routine upon its first introduction in January, affording students the opportunity to practice procedures associated with number talks. One of the first things witnessed by Emily was observing Mrs. Piper raise her hand, followed by raising her thumb, to model for students how they could show that they wanted to share their thinking with the class. Mrs. Piper encouraged students to practice these actions (Classroom Observation 1, January 21, 2020). Following several rounds of modelling these actions, Mrs. Piper asked, “Do we yell [the answer] or keep [the answer] in our head?” (Observation 1, January 21, 2020) to which the students collectively replied that they keep the answer in their head. To practice how she wanted the students to respond instead of shouting out, Mrs. Piper asked them to show her by raising their thumbs (Observation 1, January 21, 2020). Reminders about procedures became a regular part of the number talk routine before Mrs. Piper showed students the first visual dot pattern to be discussed.
Students responded positively to Mrs. Piper’s efforts to engage them in understanding how to participate during number talks. When asked during the post-interview how he showed his thinking to others in math, Thomas replied “You can talk to them” (Thomas’s Interview 2, February 25, 2020). Like Thomas, Elizabeth also stated that they got to “switch tables” to talk to different students (Elizabeth’s Interview 2, February 26, 2020). These examples from two of the post-interviews suggest that, for both Elizabeth and Thomas, talking to others to show their thinking was a practice with which they identified.
The number talk routine had practical considerations as well. For example, Mrs. Piper typically taped a visual representation on the whiteboard at the front of the class and then covered it with a clear sheet of plastic. This clear sheet allowed Mrs. Piper to erase the response from the previous student before the next student came up to show their thinking. Given that students were circling their groupings with a marker, there was the potential for confusion amongst the students if they were trying to create their own groupings amongst previous work. This practice also enabled Mrs. Piper to monitor who had participated. Mrs. Piper chose two students to answer each question, taking into consideration who had not shared. Once a question had been answered by two students, Mrs. Piper replaced the paper with a different dot pattern visual (Classroom Observation 1, January 21, 2020). As Mrs. Piper displayed the next question, she praised students collectively for their willingness to participate (Classroom Observation 1, January 21, 2020) or made general comments about the dot pattern visual to be discussed (Classroom Observation 3, January 29, 2020).
Students responded well to Mrs. Piper’s efforts to make number talks familiar to them. When asked during an interview about the routine, Thomas explained that “[Mrs. Piper] also says make rows and then some of us get a turn to circle the numbers” (Thomas’s Interview 2, February 25, 2020). As Thomas’s explanation indicates, he understood that number talks involved sitting in rows on the ground and that some students were called upon to explain their thinking by circling groups of dots using a whiteboard marker. Mrs. Piper’s practice of consistent number talk procedures was a pattern regularly observed and it afforded students the opportunity to internalize this routine and normalize the practice of sharing their thinking.
While Mrs. Piper made sure to explicitly review the number talk routines with her class, students created their own number talk behaviours— behaviours that were consistently observed across the observations. For example, Mrs. Piper never stated that students should represent their thinking in different ways for each dot pattern visual. At the same time, she also did not state that students were allowed to share the same mathematical thinking as a previous student. It was consistently observed that students felt their ideas had to be different from what was shared by the previous student. For both Thomas and Elizabeth, it was observed that the solution they presented to the class did not always make the most sense to them and they relied on Mrs. Piper’s prompting to assist them in organizing their thinking. Both students indicated in their interviews that they saw their role as sharing their thinking with Mrs. Piper so that she would know how they did and what to do if their thinking did not make sense. Thomas and Elizabeth generally waited for Mrs. Piper to ask them to explain what they had done, as this seemed to be another unofficial classroom norm during number talks.
These data are interconnected examples of how students responded to Mrs. Piper’s efforts to make number talks a regular part of their mathematics learning. The infusion of IQ principles was present in each number talk as Mrs. Piper showed ways for students to indicate their desire to share ideas (pilimmaksarniq: using different means to learn), engaged them in discussion about how to participate (Aajiiqatigiinniq: making decisions through discussion), and had the students work together to achieve common understanding about participation and sharing their thinking (Piliriqatigiinniq: collaborating together to achieve a goal). Striking in student responses to Mrs. Piper’s efforts to routinize number talks was their knowledge of its procedures and their reliance on her, rather than their peers, to provide further prompting if they were uncertain.
From the beginning of the observations, the Grade 1 students seemed to be comfortable interacting with dot patterns that were displayed in a ten-frame or loosely on the page. Prior to the introduction of number talks, Mrs. Piper, using her knowledge of the IQ Principle Pilimmaksarniq (using different means to learn), had modelled to students throughout the year different ways to solve dot problems. Figure 1 provides an example of the dot patterns used. Students understood that during a number talk they were to show and talk about, how to put the dots into groups to determine how many dots there were altogether. Mrs. Piper generally asked the students at the start of each question “How many dots are there altogether” (Classroom Observation 2, January 27, 2020).
Example of a Visual Representation Used in Number Talks in Mrs. Piper’s Classroom

Students seemed comfortable with the physical act of grouping dots; yet, when it came to articulating their rationale for these groupings, some in the class struggled to explain their thinking and provide the total number of dots present in the dot pattern. In such moments, Mrs. Piper tended to take over the explanation for the student or she asked the whole class to determine the number of dots based on what a student had started (Classroom Observation 5, February 4, 2020). When Mrs. Piper offered prompts, she sometimes spoke directly to the student who was engaged in the number talk and sometimes she directed her question to the whole class. An example of how Mrs. Piper engaged the whole class occurred on February 4, 2020, as the following field note describes:
Grade 1 student, Marsha, explained that she “…did 3, 2, 2, 2, 3” to solve the problem, referring to the groups of 3 and groups of 2 she had circled on the board. Mrs. Piper prompted the students to skip count by 2s altogether to determine how many dots there were. After Mrs. Piper’s direction, the students counted “2, 4, 6,” and Mrs. Piper then had them add the 2 groups of 3s. (Classroom Observation 5)
In this fieldnote, it was observed that Mrs. Piper chose to prompt the whole class to consider how to determine the total number of dots rather than working individually with the student, Marsha.
Mrs. Piper also prompted students to explain their thinking, as was evident in the sixth classroom observation on February 6, 2020. One of the students, Carole, had circled parts of the whole to show how she got the answer but did not explain her thinking either verbally or through a number sentence (Classroom Observation 6). Mrs. Piper prompted her by asking where she had started, which encouraged Carole to point at the group of 2, then the group of 1, and finally the group of 3. When Mrs. Piper saw that Carole still was not explaining her thinking after prompting, Mrs. Piper took over and wrote the number sentence on the board (Classroom Observation 6, February 6, 2020). Mrs. Piper tended to take over the explanation process when she saw that students were not responding to her prompting, sometimes directing the questions to the whole class. This might be due to her knowledge of specific students and their reluctance to speak in front of the class, or it may have been influenced by the specific situation in which she can see the student is struggling to articulate their thoughts. Viewing Mrs. Piper’s pedagogy through the IQ principles brings to light her knowledge about the importance of relationships with others (Inuuqatigiitsiarniq), being welcoming and inclusive (Tunnganarniq), and her efforts to encourage students to make decisions through discussion (Aajiiqatigiinniq) and collaboration (Piliriqatigiinniq).
For Elizabeth and Thomas, Mrs. Piper’s practices had some effect on their understanding of number talks. For example, when asked what mathematics looked like in his classroom, Thomas stated “Mrs. Piper puts numbers up and we have to count them and then raise our hand and do away by circling them” (Thomas’s Interview 2, February 25, 2020). During the first interview with Elizabeth, her familiarity with dot patterns was evident when asked how she showed her thinking to others in mathematics. She replied “I … show my picture to everybody. It’s like 4 red dots and 3 blue dots and then we take away 3” (Elizabeth’s Interview 1, January 17, 2020).
Throughout the eight classroom observations, students in the Grade 1 class demonstrated their familiarity with dot patterns as well as their growing familiarity with number talks. Each number talk had the students determine how many dots there were altogether. Prior to the introduction of number talks, students were familiar with seeing dot patterns in their mathematics class. With the introduction of number talks, students learned new practices associated with number talks to engage with the dot patterns. Mrs. Piper, making use of the IQ principle Pilimmaksarniq (using different means to learn), had modelled to students throughout the year how to make use of different practices. Also, prior to the introduction of number talks, she used different ways, or Qanuqtuurniq (resourceful problem solving), to solve dot problems. The students used that mentorship during the implementation of number talks to circle groups of dots to find the total number of dots. By the end of the study, students understood the routines associated with number talks and were able to share, often with assistance from Mrs. Piper, how they grouped the dots in the dot patterns to determine the total number of dots.
When talking with Thomas during the first interview, it was evident that he was developing an understanding of mathematics as a subject. During Thomas’s first interview, he explained that in mathematics “you have to try to spell and try to use your sounds” (Thomas’s Interview 1, January 21, 2020). When asked again what mathematics looked like in their class, Thomas replied “Mrs. Piper helps us figure out the words. I write about pictures” (Thomas’s Interview 1, January 21, 2020). A month later in his second interview, his understanding of mathematics as a discipline had evolved. When asked how he felt about number talks, he replied: “Good. I liked counting numbers and doing math and I like spelling my words” (Thomas’s Interview 2, February 25, 2020). These conversations with Thomas show his emerging understanding of mathematics, as well as how it was emerging.
Elizabeth’s understanding of mathematics as a subject area was more developed at the start of the study. During the first interview with Elizabeth, it was evident that she understood mathematics generally, as demonstrated in the following example. In response to the question, what does mathematics look like in your classroom, Elizabeth picked up Emily’s iPod and placed it beside her little finger and offered, “Measuring our pinky and something taller. Which one is taller: the phone or my pinky?” (Elizabeth’s Interview 1, January 17, 2020). During Elizabeth’s second interview, her explanation of what mathematics looked like in the classroom became more technical and she described its activities as doing “like equals and plus and minus” (Elizabeth’s Interview 2, February 26, 2020).
During classroom observations, it was observed that while students’ number sense understanding gradually developed, they did not always use the specialized language of mathematics when they explained how they had grouped the dots in the visual. Instead, many of the students said that they “…did 3, 2, 2, 2, 3” to explain their process instead of saying that they added the numbers or that they did 3+2+2+2+3 to find the total number of dots (Classroom Observation 5, February 4, 2020). Most students did not put numbers into addition sentences on the whiteboard to show the final answer to their classmates nor did they explain how they had added groups of dots to determine a total number of dots. Students tended to not use the specialized language of mathematics even though Mrs. Piper modelled it in class. Mrs. Piper would say “What is 2+2+1?” (Classroom Observation 8, February 13, 2020) when assisting students with explaining their thinking, and it was very rare for a student to include the answer in their explanation without requiring prompting from the teacher. One of the few examples was when the Grade 1 student, Mark, explained that “[he] did a 3 and the 8 and then [he] put it together and it makes 10” (Classroom Observation 4, January 30, 2020).
One of the goals of number talks is to help students develop their number sense (Hufferd-Ackles et al., 2004). By introducing students to the routines around number talks, such as sharing their thinking with the class, students are afforded opportunities to learn from each other. Both Thomas and Elizabeth’s, as well as the other student participants’, general understandings of number sense and mathematics as a discipline seemed to benefit from their participation in number talks. Over the course of the study, their understanding of number sense and mathematics as a subject area, while emerging, was evident for most students, including Elizabeth and Thomas. While some of the students, like Thomas, seemed to be timid and tended to take their lead from Mrs. Piper’s prompts for most of the number talks, others, like Elizabeth, were able to explain their thinking to their peers without her assistance. The students in the class adapted well to the number talk routines that were explicitly taught by Mrs. Piper and they also adhered to socially constructed, unofficial, number talk norms that were never directly taught by the classroom teacher. For example, students felt they should show their thinking in a different way than the previous students if they got a turn to share. Some of the students also seemed to think that they needed to wait for Mrs. Piper to ask them to share their thoughts before they could begin. If students had trouble articulating their thinking to the class, Mrs. Piper tended to take over the explanation for them or she enlisted the class to help them determine the total number of dots. Students in this Grade 1 class did not generally use the specialized language of mathematics during the number talks, even though the teacher consistently modelled these terms with the students. Through further exposure to daily number talks, it seems plausible that students will become more accustomed to justifying and defending their answers and continue to develop their number sense.
Scholars have noted the importance of number talks as a strategy to bolster student willingness to engage in talk about their mathematics learning (Murata et al., 2017; Sun et al., 2018). The implementation of number talks has been found to improve two essential mathematics elements, number sense and procedural fluency (Matney et al., 2020), as students are given time in conversation with each other to practice number concepts (Postlewait et al., 2003). Maintaining a focus on how Inuit students responded to the use of number talks in a Grade 1 classroom in Nunavut required exploring student interactions and perspectives in response to the pedagogical decision-making of their teacher. With the introduction of number talks, students developed the understanding that there are multiple ways to solve a problem. Students were also expected to explain their thinking to the class instead of simply sharing the answer. We have shown how important Mrs. Piper was to students’ emerging understanding of the number talk routine in how she worked at establishing its procedures and norms (Parrish, 2014). As Murata et al. (2017) found, the teacher’s pedagogical decisions can impact the effectiveness of number talks in the classroom. While Mrs. Piper implemented the routines of number talks and used purposeful problems, other aspects of number talks were less successfully cultivated, such as encouraging discussion amongst the students when multiple answers are presented (Bennett, 2014; Henning et al., 2012).
Investing time to ensure students understand the routine, however, allowed students to anticipate its procedures and Mrs. Piper’s expectations while also developing their own “rules” on how to share their thinking in the act of not replicating one another’s ideas. By encouraging students to explain their thinking, Mrs. Piper was helping students to develop a better understanding of the concepts being taught (Cavanna et al., 2015). While our findings are reminiscent of other studies (Bennett, 2014; Hufferd-Ackles et al., 2004; Matney et al., 2020; Parrish, 2014), our contribution reveals the positive possibilities of number talks as an important strategy to include in the teaching of elementary mathematics in Nunavut.
The eight IQ principles are used as the foundation of education in Nunavut (Nunavut Department of Education, 2007). Even though the strategy of number talks was not created with these IQ principles in mind, the strategy, arguably, aligns with six of the eight IQ principles in their structure and philosophy. For example, if used effectively, number talks are inclusive of all students and provide various entry points to solve the problem as there is no right way to answer the question (Parrish, 2014; Sun et al., 2018). Students are taught the procedure around number talks which includes being respectful of others’ ideas, even when contradictory responses are offered (Bennett, 2014; Hufferd-Ackles et al., 2004; Matney et al., 2020; Parrish, 2014). If there are multiple answers presented by students, the students must justify and defend their responses in a way that allows the class to come to a consensus on justifications for correct answers (Bennett, 2014; Henning et al., 2012; Matney et al., 2020; Parrish, 2011). For those students who are unsure of how to approach the problem, they are provided with the opportunity to learn from their peers as their peers explain their thinking to the class (Bennett, 2014; Hufferd-Ackles et al., 2004; Stott & Graven, 2015). Students are encouraged to be resourceful and to come up with the best way for them to explain their rationale (Bennett, 2014; Matney et al., 2020; Parrish, 2014). While beyond the scope of this study, exploring the question of whether Inuit students (or others from their community) see a meaningful connection between the IQ principles and the processes and actions within number talks, and other strategies adopted from the South, is a critical consideration for future research.
When assessing whether a Southern practice is relevant to Inuit student learning, or whether it can be adapted, the IQ principles form a crucial teacher pedagogical framework to enhance the elements of respect and relevance (Kirkness & Barnhardt, 1991). It cannot be assumed, however, that a Southern strategy is culturally relevant simply because it has resonance with some or all the IQ principles. While understanding this relationship is important, it is not the only step that must be taken when ensuring a strategy is culturally relevant. For example, we cannot assume that our, and Mrs. Piper’s, interpretation and thinking about the IQ principles is fulsome or, even, always culturally appropriate or respectful. We acknowledge that many Indigenous communities and researchers struggle when non-Indigenous researchers draw conclusions in relation to their cultures when they do not themselves have the Indigenous knowledge2. At the same time, we are mindful that it is a common practice for teachers to be recruited to Nunavut from the South due to the present lack of Inuit teachers (Government of Nunavut, 2021; Preston, 2016; Ramussen, 2011). It appears that curricula and teaching practices developed in southern contexts will continue to be offered in Nunavut. In the Nunavut Education Act, it is stated that the IQ principles must be the foundation of all school programs (Consolidation of Education Act, 2020). Perhaps it is an optimistic goal that incorporating IQ principles into the daily teaching of Nunavut educators will disrupt Eurocentric teaching methods (Fredua-Kwarteng, 2016; McGregor & McGregor, 2016). Yet, we suggest that it is encouraging to think that this research helps interrogate a southern strategy in a new, culturally relevant light. We offer what we hope may be viewed as a middle ground in how the IQ principles offer a valuable way to assess the possibilities of a teaching strategy developed in other educational contexts. Such an assessment process, along with professional development opportunities, community involvement, and feedback from Elders and parents, might be included as the next and necessary steps, essential pieces informing a larger puzzle towards accountability, reclamation and revitalization. Our hope is that the findings of this study will resonate with others in this educational context and might resonate with others in similar teaching situations outside of the North.
1 The names of the students and the teacher are pseudonyms. In consultation with the students, their pseudonyms are Western in origin (as are their real names) to reflect a common practice of many families in the schooling community.
2 Our thanks to the reviewer for this insightful point.
Aylward, M. L. (2007). Discourses of cultural relevance in Nunavut schooling. Journal of Research in Rural Education, 22(7), 1-9. https://jrre.psu.edu/
Aylward, M. L. (2009). Culturally relevant schooling in Nunavut: Views of secondary school educators. Études/Inuit/Studies, 33(1/2), 77-93. https://www.jstor.org/stable/42870290
Aylward, M. L. (2010). The role of Inuit languages in Nunavut schooling: Nunavut teachers talk about bilingual education. Canadian Journal of Education, 33(2), 295-328. https://www.jstor.org/stable/canajeducrevucan.33.2.295
Berger, P. (2009). Eurocentric roadblocks to school change in Nunavut. Études/Inuit/Studies, 33(1-2), 55-76. https://doi.org/10.7202/044960ar
Bergquist, K. (2020). Local Mathematics in Nunatsiavut: A Funds of Knowledge Approach [Unpublished doctoral dissertation]. University of Ottawa. https://ruor.uottawa.ca/bitstream/10393/40752/1/Bergquist_Karli_2020_thesis.pdf
Boaler, J. (2002). Learning from teaching: Exploring the relationship between reform curriculum and equity. Journal for Research in Mathematics Education, 33(4), 239-258. https://doi.org/10.2307/749740
Boaler, J. (2015). Fluency without fear: Research evidence on the best ways to learn math facts. https://www.youcubed.org/evidence/fluency-without-fear/.
Castagno, A. E., & Brayboy, B. M. J. (2008). Culturally responsive schooling for Indigenous youth: A review of the literature. Review of Educational Research, 78(4), 941-993. https://doi.org/10.3102/0034654308323036
Cavanna, J. M., Herbel-Eisenmann, B., & Seah, W. T. (2015). Investigating teachers' appraisal of unexpected moments and underlying values: An exploratory case in the context of changing mathematics classroom discourse. Research in Mathematics Education, 17(3), 163-182. http://dx.doi.org/10.1080/14794802.2015.1112301
Consolidation of Education Act, S.Nu. 2008, c.15 (2020). Retrieved from https://gov.nu.ca/sites/default/files/conssnu2008c15.pdf
Esmonde, I. (2009). Explanations in mathematics classrooms: A discourse analysis. Canadian Journal of Science, Mathematics and Technology Education, 9(2), 86-99. https://doi.org/10.1080/14926150902942072
Forman, E., McCormick, D., & Donato, R. (1997). Learning what counts as a mathematical explanation. Linguistics and Education, 9(4), 313-339. https://doi.org/10.1016/s0898-5898(97)90004-8
Fredua-Kwarteng, E. (2016). Inuit voices on quality education in Nunavut: Policy implications. International Journal of Educational Methodology, 2(1), 31-44. https://doi.org/10.12973/ijem.2.1.31
Gay, G. (2013). Teaching to and through cultural diversity. Curriculum Inquiry, 43(1), 48-70. https://doi.org/10.1111/curi.12002
Gee, J. (2005). An introduction to discourse analysis theory and method (2nd ed.). Routledge. https://doi.org/10.4324/9780203847886
Government of Nunavut. (2021). 2020-2021 Annual Report, Department of Education. 2022-11-08-Department-of-Education-2020-2021 Annual Report -eng.pdf (assembly.nu.ca)
Henning, J. E., McKeny, T., Foley, G. D., & Balong, M. (2012). Mathematics discussions by design: Creating opportunities for purposeful participation. Journal of Mathematics Teacher Education, 15(6), 453-479. https://doi.org/10.1007/s10857-012-9224-1
Herbel-Eisenmann, B., Lubienski, S., & Id-Deen, L. (2006). Reconsidering the study of mathematics instructional practices: The importance of curricular context in understanding local and global teacher change. Journal of Mathematics Teacher Education, 9(4), 313-345. https://doi.org/10.1007/s10857-006-9012-x
Hufferd-Ackles, K., Fuson, K. C., & Sherin, M. G. (2004). Describing levels and components of a math-talk learning community. Journal for Research in Mathematics Education, 35(2), 81-116. https://doi.org/10.2307/30034933
Inan, B., & Yuksel, D. (2013). Teaching and learning as a linguistic process: Social interactionist/ sociocultural perspectives on the study of uptake. Dil Ve Edebiyat Egitimi Dergisi, 2(7), 103-115. https://arastirmax.com/en/publication/dil-edebiyat-egitimi-dergisi/2/7/103-115-teaching-and-learning-linguistic-process-social-interactionist-sociocultural-perspectives-study-uptake/arid/c4fa7947-8e19-43b3
Kirkness, V. J., & Barnhardt, R. (1991). First Nations and higher education: The four R's—Respect, relevance, reciprocity, responsibility. Journal of American Indian Education, 30(3), 1-15. https://jaie.asu.edu/
Ladson-Billings, G. (1995). Toward a theory of culturally relevant pedagogy. American Educational Research Journal, 32(3), 465-491. https://doi.org/10.3102/00028312032003465
Ladson-Billings, G. (2014). Culturally relevant pedagogy 2.0: aka the remix. Harvard Educational Review, 84(1), 74-84. https://doi.org/10.17763/haer.84.1.p2rj131485484751
Lipka, J. (1994). Culturally negotiated schooling: Toward a Yup'ik mathematics. Journal of American Indian Education, 33(3), 14-30.
Lipka, J., Hogan, M. P., Webster, J. P, Yanez, E., Adams, B., Clark, S., & Lacy, D. (2005). Math in a cultural context: Two case studies of a successful culturally based math project. Anthropology & Education Quarterly, 36(4), 367-385. https://doi.org/10.1525/aeq.2005.36.4.367
Matney, G., Lustgarten, A., & Nicholson, T. (2020). Black holes of research on instructional practice: The case of number talks. Investigations in Mathematics Learning, 12(4), 246-260. https://doi.org/10.1080/19477503.2020.1804273
McCarty, T., & Lee, T. (2014). Critical culturally sustaining/revitalizing pedagogy and Indigenous education sovereignty. Harvard Educational Review, 84(1), 101-124. https://doi.org/10.17763/haer.84.1.q83746nl5pj34216
McGregor, H. E., & McGregor, C. A. (2016). Behind the scenes of Inuit curriculum development in Nunavut, 2000–2013. Études Inuit Studies, 40(2), 109-131. https://doi.org/10.7202/1055434ar
McIntosh, A., Reys, B. J., & Reys, R. E. (1992). A proposed framework for examining basic number sense. For the Learning of Mathematics, 12(3), 2-44. chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://flm-journal.org/Articles/94F594EF72C03412F1760031075F2.pdf
Merriam, S. B., & Tisdell, E. J. (2016). Qualitative research: A guide to design and implementation (4th ed.). Jossey-Bass.
Mitton, J., & Murray-Orr, A. (2021). Identifying the impact of culturally relevant pedagogy: Evidence of academic risk taking in culturally and economically diverse Nova Scotia classrooms. Canadian Journal of Education, 44(4), 1084-1115. https://journals.sfu.ca/cje/index.php/cje-rce/article/view/4811/3085
Morgan, C., & Sfard. A. (2016). Investigating changes in high-stakes mathematics examinations: A discursive approach. Research in Mathematics Education, 18(2), 92-119. https://doi.org/10.1080/14794802.2016.1176596
Munroe, E. A., Lunney Borden, L., Orr, A. M., Toney, D., & Meader, J. (2013). Decolonizing aboriginal education in the 21st century. McGill Journal of Education, 48(2), 317-337. https://doi.org/10.7202/1020974ar
Murata, A., Siker, J., Kang, B., Baldinger, E. V., Kim, H., Scott, M., & Lanouette, K. (2017). Math talk and student strategy trajectories: The case of two first grade classrooms. Cognition and Instruction, 35(4), 290-316. https://doi.org/10.1080/07370008.2017.1362408
Nunavut Department of Education. (2007). Inuit Qaujimajatuqangit: Education Framework for Nunavut Curriculum. Nunavut Department of Education, Curriculum and School Services Division.
Nunavut Department of Education. (2019). 2019–2020 Nunavut Approved Curriculum and Teaching Resources. [Curriculum Development Presentation]. chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://www.gov.nu.ca/sites/default/files/documents/2022-03/2019-20_nunavut_approved_curriculum_and_teaching_resources.pdf
Paris, D. (2012). Culturally sustaining pedagogy: A needed change in stance, terminology, and practice. Educational Researcher, 41(3), 93-97. https://doi.org/10.3102/0013189x12441244
Paris, D., & Alim, H. S. (2014). What are we seeking to sustain through culturally sustaining pedagogy? A loving critique forward. Harvard Educational Review, 84(1), 85-101, 134, 136-137. https://doi.org/10.17763/haer.84.1.982l873k2ht16m77
Parrish, S. D. (2011). Number talks build numerical reasoning. Teaching Children Mathematics, 18(3), 198-206. https://doi.org/10.5951/teacchilmath.18.3.0198
Parrish, S. (2014). Number talks: Helping children build mental math and computation strategies, grades k-5, updated with common core connections. Math Solutions.
Poirier, L. (2007). Teaching mathematics and the Inuit community. Canadian Journal of Science, Mathematics and Technology Education, 7(1), 53-67. https://doi.org/10.1080/14926150709556720
Postlewait, K. B., Adams, M. R., & Shih, J. C. (2003). Promoting meaningful mastery of addition and subtraction. Teaching Children Mathematics, 9(6), 354-357. https://doi.org/10.5951/tcm.9.6.0354
Preston, J. (2016). Situating educational issues in Nunavut: Perceptions of school leaders and teachers. The Northern Review: Exploring Human Experience in the North, 42, 109-129. https://doi.org/10.22584/nr42.2016.007
Rasmussen, D. (2011). Forty years of struggle and still no right to Inuit education in Nunavut. Interchange, 42, 137-155. https://doi.org/10.1007/s10780-011-9152-5
Russell, G, L., & Chernoff, E, J. (2013). The marginalisation of Indigenous students within school mathematics and the math wars: Seeking resolutions within ethical spaces. Mathematics Education Research Journal, 25(1), 109-127. https://doi.org/10.1007/s13394-012-0064-1
Sfard, A. (2007). When the rules of discourse change, but nobody tells you: Making sense of mathematics learning from a commognitive standpoint. Journal of the Learning Sciences, 16(4), 565-613. https://doi.org/10.1080/10508400701525253
Stott, D., & Graven, M. (2015). Adapting number talks to foreground mathematical progression in South African classrooms. In J. Novotná & H. Moraová (Eds.), Developing mathematical language and reasoning - International Symposium Elementary Maths Teaching (pp. 311-321). Charles University, Faculty of Education.
Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Harvard University Press.