
Gesturing and Image Making: Growing Mathematics Understanding
Marc Husband, Lisa Lunney Borden, and Evan Throop Robinson
St. Francis Xavier University
Authors’ Note
Marc Husband https://orcid.org/0000-0002-3593-1097
Lisa Lunney Borden https://orcid.org/0000-0003-1116-429X
Evan Throop Robinson https://orcid.org/0000-0003-1116-429X
Correspondence regarding this article should be directed to Marc Husband. Email: mhusband@stfx.ca
_____________________________
In the Principles to Action document, the National Council of Teachers of Mathematics (NCTM) (2014) recommended that teachers "elicit and use evidence of student thinking” (p. 10). But how do teachers gain insight into what goes on in the minds of students? To assess progress toward understanding, teachers must know what is important to notice, plan for such noticings, and use this information to make instructional decisions (NCTM, 2014). Knowing what matters in determining students’ understanding can be challenging. Teachers often pay attention to products created by students or to oral explanations given by students after they have completed a task; however, we think it is important for teachers to pay close attention to students’ use of non-verbal resources, such as gesturing as they are doing a task. Students’ ideas can be captured by such in-the-moment observations of not only what students say but also by what they do. Despite calls to use evidence of students’ thinking, little research details how the effective use of the body—particularly gesture—might afford teachers insight into student thinking in real time.
Williams-Pierce et al. (2017) identified three pedagogic needs for teachers: (a) to appreciate more fully the role of gestures in developing mathematical understandings, (b) to determine ways to capture the gestures through tasks and assessments, and (c) to use information from gestures in real time. In our work, we have been thinking about the ways in which we can make student thinking visible and have drawn upon existing data to consider the role of gestures in this process. While a large body of literature emphasizes the importance of gestures in mathematics, few researchers show examples of teachers paying attention to and using gestures for assessment. We argue that paying attention to students’ gestures can assist teachers in understanding students’ thinking by noticing not only what students are saying but also what they are doing.
The purpose of this paper is to highlight two examples of how students use gestures to respond to teachers’ requests to demonstrate what they know. We argue that the types of tasks or investigations that teachers select can elicit these kinds of non-verbal expressions, which in turn, allow teachers to observe ideas that can support growth in mathematical understanding.
Using Gestures to Express Mathematical Thinking
Current mathematics education research recognizes gestures, long used informally to augment or replace speech (i.e., hand and body actions or movements), for their importance in growing mathematical understandings (Towers & Martin, 2015). Radford (2009) theorized that thinking does not happen only “in the head but in and through language, body, and tools” and that these “are genuine constituents of thinking” (p. 113). Through his description of research on Grade 10 students’ sign usage, Radford highlighted the importance of gestures, utterances, and various tools while working through a mathematical task. He argued that individual learners demonstrate their thinking through the use of gestures not only to serve to make something visible to others but also to promote mathematical thinking.
Multimodality
In considering the role of gestures, we recognize that a large body of literature refers to the notion of multimodality: semiotic resources are used concurrently in making and conveying meaning (Arzarello et al., 2009; Wu, 2014), which includes gesturing. For example, Shreyar et al. (2010) looked at the multimodal aspects of a whole-class discussion among a teacher and Grade 6 students and discovered that the teacher’s use of a variety of semiotic resources, including diagrams, gestures, and speech, guided students’ mathematical understanding of the concept of percentages. Samson and Schafer (2011) analysed a high school student’s visualization of a geometric pattern. They found that a fruitful visualization—one that is and will lead to a general rule—was reached through a combination of linguistic devices, metaphor, gestures, rhythm, and symbolic expressions. Arzarello et al. (2009) also explored meaning-making in the context of using a variety of modes. In their research with Grade 11 students, they noted, “the complex intertwining among gestures, speech, and inscriptions in learning mathematics” and that these “jointly support the thinking processes of students” (pp. 106–107). Similarly, Radford (2008) discussed how actions, gestures, and words work together to construct knowledge. So, while all modes of expression are important in conveying meaning, gestures are key in each of these examples. Thus, we agree with Edwards (2009), that gestures are a significant mode through which to represent thinking and may have a powerful influence on learning mathematical concepts.
In our own work, we draw from Pirie Kieren's theory and Indigenous knowledge systems rooted in verbing to support teachers in the classroom. Much of our work involves helping teachers to act in real time, observing and listening for students’ in-the-moment thinking and making pedagogical decisions about the kinds of experiences that support growth in students’ mathematical understanding. We believe that gestures play an important role in both of these theoretical underpinnings of our work.
Theoretical Underpinnings: Bringing Together Image Making and Verbing
Pirie-Kieren (P-K) Theory
Researchers Pirie and Kieren (P-K) (1994) developed a theory to explain how we learn mathematics. P-K theory, as it is referred to, tells us that growth in understanding occurs in non-linear ways through eight layers of understanding. They name these layers: primitive knowing, image making, image having, property noticing, formalising, observing, structuring, and inventizing. P-K theory is helpful because it explains how learning is flexible and dynamic. Students continuously move between and among layers, using and revisiting what they already know to grow understanding. For this paper, we focus on the image making layer, where the emphasis is on students using what they know in new ways as they generate ideas to grow their understanding.
Image Making
In P-K terms, the word “image” is not a picture; rather, it comprises all the ideas that emerge through learning experiences involving concrete materials, symbols, pictures, or other visuals, including gestures. Image making involves actions—doing, reviewing, seeing, and saying—as students construct their understanding. To grow mathematics understanding, in P-K theory, value is placed on learners making and using a rich image (or idea) to make connections by noticing important mathematical properties. For example, when learning multiplication, students might build an area model, make a set model, explore jumps on a number line, or look for number patterns on a hundreds chart, and so on. So, image making is not just about building or making these representations but also looking across these representations to see emerging ideas about multiplication (see Lunney Borden et al., 2021). As such, we argue that the concept of image making is important because when teachers are selecting tasks for students, it is necessary to consider how the task will evoke a variety of images, including actions (gestures).
Verbing Mathematics
Image making aligns with ideas from a second theory we draw from in our analysis, namely verbing mathematics (Lunney Borden, 2011). Verbing was inspired by the verb-based nature of Indigenous languages as a culturally consistent approach to mathematics teaching and learning. Lunney Borden (2011) advocated for paying attention to the actions and processes involved in mathematics. For example, teachers provide experiences for students to engage in joining and separating using concrete materials rather than focusing on the sum or the difference. Verbing mathematics directly contradicts the tendency toward using too many nouns to describe processes (actions). Rather than focusing on the nouns of an artifact like an array (i.e., asking about the dimensions or area), we focus on the verbing by bringing attention to the making of or the forming of the array. Attending to processes allows the image making to be an ongoing movie rather than a still image. This might look like a student seeing the action of moving counters together to make a 10 when joining six counters and five counters. A teacher might also see a student repeatedly gesturing to show how these sets of counters came together to make the 10. This is how gestures can help teachers to see image making as moving pictures.
Selecting a Task
Smith and Stein (1998) explained the importance of using specific criteria for selecting tasks to promote higher-level cognitive demands. One criterion involves making connections using multiple representations—visual diagrams, manipulatives, symbols, and problem situations. Smith and Stein (2018) elaborated on teachers selecting a task by saying that using a manipulative or diagram helps to develop mathematical ideas as students work on the task. While many researchers discuss the value of using contextualized problems alongside the manipulative or diagram, the tasks selected in this paper avoid contrived situations and instead use mathematical ideas itself as the context. In both videos, the mathematical objects are the context for the thinking. The task in Video 1 was specifically designed to draw from verbing mathematics as a way to support student learning. Similarly, the task in Video 2, was designed to focus attention on growing patterns. It is worth noting that these tasks also evoked gesturing as students engaged with them.
Methods: Video Analysis
As part of professional meetings about ongoing inquiries into the teaching and learning of mathematics, we discussed how teachers come to know and understand what children are thinking with respect to the mathematics they are learning. We revisited two video clips from the two different projects on several occasions and were fascinated by the gesturing in each video. While the two studies in question utilized different methodological approaches and had different purposes, both took up this idea of how teachers and learners make thinking visible. Subsequent conversations about the role of gestures in these videos led to further, more in-depth exploration of the two video clips through video analysis.
Thus, the data used in this article comes from two larger research projects. One project was designed to decolonize mathematics teaching and learning in an Indigenous context, drawing upon language and culture to centre L’nui’ta’simk (L’nu or Mi’kmaw ways of knowing, being, and doing, in particular, verbing). This project brought researchers together with teachers in Mi’kmaw schools to implement lessons designed to help students build understanding of concepts in culturally consistent ways. Decolonizing mathematics teaching and learning involves honoring students' cultural ways of knowing, being, and doing as they engage in learning. In this particular instance, the focus was on drawing from the verb-based nature of the Mi’kmaw language to design tasks rooted in a verbing approach. The video clip selected for further analysis comes from a Grade 3 classroom where Lisa had worked with teachers to develop a set of learning centers focused on building an understanding of multiplication through verbing (e.g., Lunney Borden et al., 2021). The videos collected documented several moments of interaction with the tasks. One of these tasks, “building rows of,” is used in this paper.
The other project focused on creating a professional learning community for inquiries into mathematics education. Practicing teachers, administrators, researchers, and graduate students met weekly for 12 weeks. As part of the course, in-service teachers participated in weekly video club meetings to share short video clips that addressed specific inquiry topics from their classrooms. The video clip selected for further analysis in this paper was initially brought to the video club by one of the teacher participants because it provoked a rich conversation about the student’s use of gestures.
We adapted Powell et al.’s (2003) analytical model for studying gestures for our video data analysis. Their seven phases are: viewing the video data attentively, describing the video data, identifying critical events, transcribing, coding, constructing a storyline and composing a narrative. A researcher may go back and forth through these phases. The following phases unfolded as we studied the video data:
Coincidentally, both examples look at students using an array, a rectangular arrangement of objects in rows and columns, to represent multiplication. In the first example, the student works on building an image for multiplication and developing counting strategies to determine the total. In the second example, the student uses an array to explore patterns and determine a pattern rule. While we engaged in these research projects separately, we noted that in both of our examples, the student first used image making to build understanding of the array, and then used the idea of an array to build understanding of the task at hand. In what follows, we first describe how each student used their images to make sense of the array. Later, we will share how they worked with the array to find a solution.
Image Making: Arrays
Sa’n’s Shaping of a Flipped L
Sa’n has rolled four and six on his two dice and has been asked to build “rows of” for this activity by choosing either four rows of six or six rows of four, using square color tiles. He builds four rows of six, though from the positioning of the camera it appears more as six rows of four. As the teacher arrives to observe, Sa'n’s area model is already created (Figure 1).
Figure 1
Sa'n’s Area Model

Note. The image shows an array of four by six
As he refers to the six squares in a row, which he calls rows, he moves his hand up and down repeatedly along the row of six squares. He then turns his attention to the other dimension and repeatedly moves his hand back and forth along the four squares, stating “four rows” (Table 1). This gesture of a flipped L along with the repeated motion along these lines is how Sa’n shows his image making of the array. While his language of rows and columns is not yet clear, what is clear is that he has an image of an array that is contained within this area bounded by his gesture. His explanation alone is insufficient to see his thinking about arrays. Rather, the gestures showing the boundaries of the array give insight into the image making, supporting his understanding of this structure.
Table 1
Sa'n’s Gestures for an Array

Serra’s Tracing the Backward L
To introduce the concept of an array, the teacher asks Serra: “D'you know what I mean when I say an array?” Serra responds by moving her hand to the middle section of term three and saying, "three across and three up.” She places three fingers on three units in the third row and then drags one finger down the third column (Figure 2).
Figure 2
Geometric Growing Pattern Task
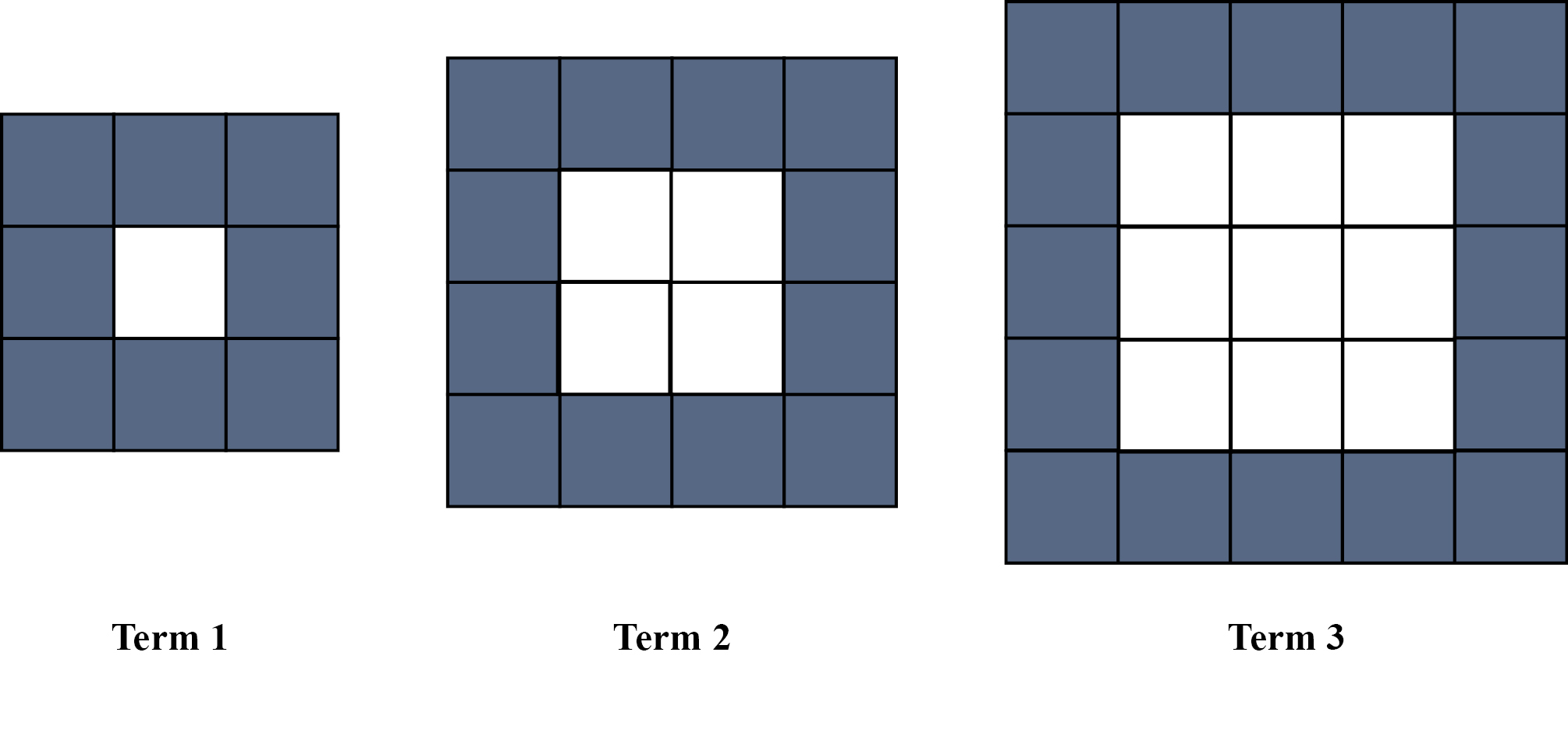
Note. Array growing pattern
Her combined words and gestures demonstrate her images about arrays—which include rows and columns. When the teacher prompts Serra for another way to describe an array, she gestures in a slightly new manner..Using her index finger, she points to the first unit in the third column, then drags her finger down three and left towards the first unit in the third row. Resembling a backward “L,” Serra’s gesture is one continuous movement that shows the boundary of the array (Table 2).
Table 2
Serra’s Gestures for an Array

Image Making: The Task
Sa’n’s Gesturing Double-Double
Following Sa’n’s demonstration of the structure of the array that he built, he does not immediately respond to the teacher’s request for a total. She then asks, “Can you figure out how much is there, altogether?” After a brief pause to find a total area or a total number of squares, he declares that there are “24!” The teacher then asks, “How did you get that?” At this point, Sa’n again demonstrates his process through gestures. He brings his hand over the first row of six and then the next row of six, stating, “Well, six and six is 12.” He then gestures, seeming to hold that image of 12, and flips it over to the next 12, stating, “And 12 more.” His gestures show how he is taking that row of six and doubling it to get 12, then taking that 12 and doubling it to get 24. His gestures demonstrate the shifts in what he is paying attention to as he calculates the total (Table 3). This shows that he has a clear image of how the double-double strategy can be applied in this context.
Table 3
S’an’s Gestures for Doubling

Serra’s Pointing to “Two by Two”
Following Serra’s demonstration of her images for arrays on the third term, the teacher prompts Serra to apply this approach to the second term by asking, “And what can you see in the second one?” Serra points to the first unit of the second row and the first unit of the second column and simultaneously says, “The second one has two by two.” Instead of tracing a backward L, Serra touches the endpoints of her backward L. Following a prompt to look at the first figure, Serra points to the one unit in the first figure and says, “one by one” (Table 4).
Table 4
Serra’s Gestures for an Array

“Are You Noticing Any Patterns Here?”
Once the teacher has observed Serra’s actions and expressions on the first three terms, he asks Serra: “So what might the 10th one have? Are you noticing any patterns here?” Again Serra gestures, but this time to an imaginary 10th term. With her index finger, she taps terms one, two, and three and then the table surface next to term three, and says, “The 10th one will have 10 by 10.” Serra has noticed a pattern and uses this to predict what the 10th space might look like. She uses images of the first three terms to describe the 10th array, seeing and gesturing beyond the physical figures in front of her (Table 5).
Table 5
Serra’s Gestures for a Pattern

Discussion
It is evident from these two examples that, as Radford (2009) indicated, the student thinking is more than “in the head but in and through language, body, and tools” (p. 113). Students communicated their ideas in multimodal ways, drawing upon the tools (tiles/blocks), their gestures, and the words they used to communicate their ideas. While focusing our attention on gesturing, we recognize that this interconnected and complex approach to task design is what created the conditions for these students to engage in the tasks in these multimodal ways..From this observation, we see three important messages for teachers emerging from the above examples: selecting the task to elicit gesturing; observing and noticing student thinking reflected in the gesturing; and drawing from the dynamic nature of gesturing to focus on the process for growing mathematical understanding. We elaborate on each of these ideas below.
Selecting the Task
As noted by Williams-Pierce et al. (2017), it is important for teachers to consider the task or investigation they will use to explore a concept and how the task can provide an opportunity to capture the gestures. Sa’n and Serra’s gestures were linked to the models; their hands were pointing to components of the model that supported their image making. The concrete objects played an essential role in growing the mathematical understanding of each student. By ensuring students have numerous ways for doing, reviewing, seeing, and saying, there is more likelihood that students will connect gestures to image making. In the tasks above, the concrete objects were not used to represent something else, they were the object of investigation. In other words, Sa’n was asked to make rows of squares rather than use the squares to represent something like tiles on a floor or chairs organized in rows. Serra was asked to continue the pattern of the linking cubes rather than using the cubes to represent something like the tiles around a pool, a commonly used task. This choice to make the concrete also the context keeps children’s attention focused on the mathematics rather than concerning themselves with what this model represents. We would later apply these models to a contextualized problem, but we wanted to first focus on the mathematical ideas that emerge from exploring the concrete materials (Smith & Stein, 2018). Selecting a task that elicits opportunities to connect gestures to models will support image making.
Observing and Noticing
The interactions between teachers and students described above are examples of how learners may use gestures to communicate about the images that are shaping their understanding. Sa’n used gestures to show how he was forming the image of the array and then how he was counting the total. His gestures show his understanding of what an array looks like as well as how the double-double strategy works in the context of the array. In Serra’s case, she is gesturing alongside what she is saying to show her understanding of rows and columns, a characteristic of an array. Using this image of an array to make a prediction, Serra extends the pattern to and provides a gesture of the 10th element in the pattern that is not visible. While Serra cannot yet articulate the solution to the problem, her gestures show the teacher she has a process to get to the solution and knows what the 10th term will look like. Like Samson and Schafer’s (2011) findings, Serra’s visualization of the geometric pattern supported her understanding by helping her to think about a more general rule. Also, Sa’n’s use of the double-double strategy was reflected in his gesture. Both students use gestures to help them explain their thinking; in fact, the gestures reveal more than what their words convey. As such, it is important for teachers to notice these gestures so that they can assess how the student’s thinking with respect to the task is being communicated by the gestures.
Focusing on Process
The gestures were in motion, showing how students’ image making was dynamic. Thus doing, reviewing, seeing, and saying are active processes aligned with the verbing of mathematics. For example, asking, “Can you figure out how much is there, all together?” or “So, what might the 10th one have?” bring the students’ attention to the action of creating mathematical images. The dynamic nature of the gesture reflects the focus on process—the mental activities that get students to the solution—rather than on a static representation that shows a solution. The students used gestures to show how they came to the solution and this is reflected in the motion of their hands. Sa’n uses his hands to show the building or forming of the array. He uses his hands again to reflect the doubling of six and six and then doubling that again. His actions retrace the process he took to come to a solution. He is not giving a static final answer, he is telling us what he did with his gestures. Similarly, Serra uses her gestures to show her thinking about rows and columns. She uses the backwards L to show how rows and columns are forming, and then repeats this with the two by two but just points to the end points. She uses this idea of rows and columns to predict the non-existent 10 by 10. Serra is focused on the forming of these arrays; they are coming into being in her gestures. We align this with verbing because a verbing approach to mathematics values the forming of mathematical ideas through such construction rather than expecting a static diagram. Thus, like P-K, we emphasize image making as not merely a static image, but rather a moving picture that is created from acting and expressing: doing, reviewing, seeing, and saying.
The dynamic nature of the gesture illustrates students' growth in mathematical understanding, thus providing the teacher a window into how students are thinking in real time (Williams-Pierce et al., 2017). Teachers often ask students to recount what they did to get a solution, yet by watching the gestures that the students used, we gained insight into their process as it retraced their thinking. Paying attention to these gestures makes student thinking observable, and provides an assessment tool for helping students bring language to that process.
Concluding Thoughts
From our discussion above, we see that teachers can select tasks that will elicit gesturing, notice how the gesturing signals the thinking, and respond to the dynamic nature of a process conveyed by the gestures to stay with students' own ideas as they guide their mathematical understandings. To stay with student ideas, means we can use students' own ways of thinking to support their learning rather than trying to channel their thinking into some predefined process. The examples of Sa’n and Serra working on a mathematical task involving arrays illustrate how students used gestures to convey the Image Making process (Pirie & Kieren, 1994). We saw a focus on action aligned with verbing (Lunney Borden et al., 2021) as the student gestures showed how the arrays were forming or patterns developing..This highlights the dynamic nature of image making. Gestures provided us with insights into how the students were thinking about the mathematical ideas even when their language was not yet able to convey these ideas. While our examples particularly focused on arrays, we believe such examples support teachers to appreciate more fully the role of gestures in developing mathematical understanding (Williams-Pierce et al., 2017) and see what it looks like to notice gestures as a viable resource for growing mathematics understanding.
References
Arzarello, F., Paola, D., Robutti, O., & Sabena, C. (2009). Gestures as semiotic resources in the mathematics classroom. Educational Studies in Mathematics, 70(2), 97–109. https://www.jstor.org/stable/40284563
Edwards, L. D. (2009). Gestures and conceptual integration in mathematical talk. Educational Studies in Mathematics, 70(2), 127–141. https://www.jstor.org/stable/40284565
Lunney Borden, L. (2011). The 'verbification' of mathematics: Using the grammatical structures of Mi'kmaq to support student learning. For the Learning of Mathematics, 31(3), 8–13. https://www.jstor.org/stable/41319601
Lunney Borden, L., Throop Robinson, E., Carter, E., & Prosper, S. (2021). Sets of, rows of, jumps of: Verbing multiplication. For the Learning of Mathematics, 41(3), 2–8.
National Council of Teachers of Mathematics (NCTM). (2014). Principles to actions: Ensuring mathematical success for all. NCTM.
Pirie, S. E. B., & Kieren, T. E. (1994). Growth in mathematical understanding: How can we characterize it and how can we represent it? Educational Studies in Mathematics, 26, 165–190. https://www.jstor.org/stable/3482783
Powell, A. B., Francisco, J. M., & Maher, C. A. (2003). An analytical model for studying the development of learners’ mathematical ideas and reasoning using videotape data. The Journal of Mathematical Behavior, 22(4), 405–435. https://doi.org/10.1016/j.jmathb.2003.09.002
Radford, L. (2008). Iconicity and contraction: a semiotic investigation of forms of algebraic generalizations of patterns in different contexts. ZDM: The International Journal on Mathematics Education, 40, 83–96. https://doi.org/10.1007/s11858-007-0061-0
Radford, L. (2009). Why do gestures matter? Sensuous cognition and the palpability of mathematical meanings. Educational Studies in Mathematics, 70(2), 111–126. https://doi.org/10.1007/s10649-008-9127-3
Samson, D., & Schäfer, M. (2011). Enactivism, figural apprehension and knowledge objectification: An exploration of figural pattern generalisation. For the Learning of Mathematics, 31(1), 37–43. https://www.jstor.org/stable/41319551
Shreyar, S., Zolkower, B., & Pérez, S. (2010). Thinking aloud together: A teacher’s semiotic mediation of a whole-class conversation about percents. Educational Studies in Mathematics, 73, 21–53. https://doi.org/10.1007/s10649-009-9203-3
Smith, M. S., & Stein, M. K. (1998). Reflections on practice: Selecting and creating mathematical tasks: From research to practice. Mathematics Teaching in the Middle School, 3(5), 344–350. http://www.jstor.org/stable/41180423
Smith, M. S., & Stein, M. K. (2018). 5 Practices for orchestrating productive mathematics discussion. NCTM.
Towers, J., & Martin, L. C. (2015). Enactivism and the study of collectivity. ZDM: The International Journal on Mathematics Education, 47(2), 247–256. https://doi.org/10.1007/s11858-014-0643-6
Williams-Pierce, C. C., Pier, E. L., Walkington, C., Boncoddo, R., Clinton, V., Alibali, M. W., & Nathan, M. J. (2017). What we say and how we do: Action, gesture, and language in proving. Journal for Research in Mathematics Education, 48(3), 248–260. http://www.jstor.org/stable/10.5951/jresematheduc.48.3.0248
Wu, S. (2014). A multimodal analysis of image-text relations in picture books. Theory and Practice in Language studies, 4(7), 1415. https://doi.org/10.4304/TPLS.4.7.1415-1420