Note. This sequence shows how students take up Ben’s doubling patterning in multiplication to represent and construct their mathematical strategy piece by piece.
Understanding Meaningful Exchanges: Mathematics Discourse Analysis and Complexity Thinking
Evan Throop Robinson
St. Francis Xavier University
A concern for classroom teachers in mathematics education is the development of meaningful discourse among students. The effective mathematics teaching practices stated in Principles to Action (NCTM, 2014) include the suggestion for teachers to facilitate meaningful mathematical discourse among students in order to build shared understandings. Canadian curriculum documents remind teachers that, “Communication is important in clarifying, reinforcing, and modifying ideas, knowledge, attitudes, and beliefs about mathematics. Students should be encouraged to use a variety of forms of communication while learning mathematics.” (NSDEECD, 2014; WNCP, 2006). Recently revised curriculum in British Columbia lists communication as a core competency across the curriculum and, specifically in mathematics, encourages students to communicate effectively “in an increasing variety of contexts, for a variety of purposes, and often with multiple audiences (BC Ministry of Education, 2019). Providing space for meaningful discourse and effective communication proves challenging for teachers working within crowded curriculum and classroom conditions, where student engagement may wane in the face of traditionally repetitive procedural tasks and mundane testing requirements.
When I was a classroom teacher, I understood the benefits for my students in participating in rich mathematical discussion. I also felt the pressures of curricular demands and time constraints which often led to a rise in student anxiety levels and to a dismal drop in student fluency, conceptual understanding and engagement (Willick, 2014). Observing the classroom as a learning collective rather than a collection of learners (Davis & Simmt, 2003) combined with my research in mathematical classroom discourse (Throop Robinson, 2016) underscored significant challenges for the mathematics teacher: What is the teacher’s role in developing the classroom discourse? How does the teacher keep students engaged in learning about mathematics, given how much conventional classrooms instruct in what to do and how to do it? What is the best way for the teacher to encourage discourse as a learner/teacher rather than as a single locus of authority? Therefore, my 2016 research on classroom complexity asked and investigated the following questions: Could changing the classroom learning environment increase student engagement as well as fluency in the discourse of mathematics? And, more specifically, could the adoption of conditions that give rise to complex learning systems increase participation in the classroom discourse?
In “Mapping Complexity in an Elementary Mathematics Classroom” (Throop Robinson, 2018), I discussed how I altered the classroom’s physical environment and the instructional methodology to create the necessary conditions for a viable system of learners. Complexity thinking in education invites researchers to investigate the classroom as a system of learners (Newell, 2008). These changes dramatically increased student interaction in terms of student movement around the classroom and in conversation. Mapping and documenting this connectivity highlighted the importance of student-centered discourse in developing shared understanding.
In this paper, I focus on the analysis of student-centered discourse through applying a discourse analysis tool I developed to analyze data from an elementary Grade 6 mathematics classroom. The purpose of the analytics tool is to understand the impact of the complex learning system on the emerging classroom discourse. It is my aspiration that teachers and teacher researchers will see the potential in their classrooms to create a complex learning system and will understand the conditions required to give rise to such a system. In particular, they will have the tools to analyze students’ meaningful exchanges by recognizing the patterns of emergence, represented by sharing, building, and exploring, which potentially will lead to the convergence of new mathematical learnings. The analytic lens introduced here contributes to the toolkit of discourse analysts and teacher researchers, who seek effective ways to increase student engagement in mathematics discourse. Therefore, my primary question is—In what ways, and to what extent, do students engage in mathematical discourse when the conditions for a complex learning system are met?
I begin with a brief overview of complexity thinking, the theoretical perspective guiding my research. I next highlight significant contributions, relevant to my question, of other researchers in the field of classroom discourse. To locate my classroom research, a description of the research context follows (i.e., setting, goals, topics and methods for analysis). However, the bulk of this paper will then focus on the use of my analytic tool and a discussion of the main findings of the discourse analysis, along with a view to possible future iterations of this study.
Theoretical Perspectives
Complex Learning Systems
This research investigates the mathematics classroom through the lens of complexity thinking. Complexity thinking enables educators to conceive of their role differently. The learning collective assumes responsibility for “taken-as-shared” knowledge (Cobb et al., 1992) that emerges less from a single body and more from a self-organizing network of learners including simultaneously students and teacher (Maas & Maas, 2005). What is required of learners is active engagement in conversation, giving rise to new ideas and ways of knowing (Miranda, et al., 2006). Informed by complexity thinking, Davis & Sumara (2006) described the learner as the collective itself rather than as the individual. As they stated, “Somehow … collectives develop capacities that can exceed the possibilities of the same group of agents if they were made to work independently” (p. 81). Complexivists refer to this phenomenon as emergence that is, in an educational context, what Wheatley & Frieze (2007) described as “a powerful cultural shift that then greatly influences behaviors and defines accepted practices” (p. 35). Such a shift brings new levels of skills and capacity for participants that were not present in individual efforts and far exceed any sum of their separate efforts. From wide-scale commentaries in education (Doll, 1993; Osberg & Biesta, 2007; Sawada & Caley, 1985) to smaller-scale classroom studies (Burns & Knox, 2011; Davis & Simmt, 2003; English, 2008) descriptions and analysis of complex learning systems, as they have come to be known, provide an alternative lens through which to view students and classrooms.
Davis & Simmt (2003) argue that the necessary minimum conditions to sustain a viable and complex learning system promote communication and productive discussion among students while strengthening student-to-student networks. The minimum conditions for complexity include, “(a) internal diversity, (b) redundancy, (c) decentralized control, (d) organized randomness, and (e) neighbor interactions” (Davis & Simmt, 2003, p. 147). When these conditions are met, emergence as a phenomenon of complexity occurs. Emergence is represented by the awareness of new possibilities, new ideas, or new ways of being. And, as the complex learning system strengthens, that which is emerging converges into a new order (Johnson, 2001; Urry, 2005).
Harrison Owen (1997), an author and large group facilitator, developed a simple meeting format that meets all of the above conditions in Open Space Technology: A User’s Guide. For my research, I adapted, due to constraints of space and student time-tables, Owen’s methodology for the classroom. Open Space Technology (OST) is an instructional methodology that relies on decentralized control, self-organization, and neighbor interactions (Owen, 1997; Throop Robinson, 2018). OST provides students the time and space to play with new ideas and ways of being, on topics of interest and in group configurations chosen by the students, in hopes of changing the discourse and generating new ways of knowing. This supports Sfard’s (2007) recognition that learning mathematics requires changing its own discourse to modify students’ existing everyday discourses. Sfard (2008) considered discourse to be a phenomenon of thinking and interpersonal communication. I adopted her conceptualization of mathematics as a discourse or form of communication that is distinguishable by its word use, visual mediators, routines, and narratives to build my own analytics tool.
As I touch upon all of the above conditions in this paper, I will focus on the student-to-student interactions and their meaningful exchanges fostered through the intervention of OST in the classroom. Understanding more fully these meaningful exchanges and their emergent patterns may provide insight into the development of meaningful discourse for teachers and promote more effective communication among students. Furthermore, the analytics tool, which I developed for the teacher-researcher, is intended to provide a lens through which the discourse is seen and analyzed.
Classroom Discourse
A significant body of research on classroom discourse provides extensive considerations of the many ways of communicating in the classroom (Barwell, 2005; Herbel-Eisenmann & Otten, 2011; Manouchehri, 2007) and the “speaking rights” of the participants (Cazden, 2001). Cazden’s conception of classroom discourse informs my research as she explores critical questions such as: Who gets to participate in classrooms? How do they participate during classroom interactions? How does the classroom discourse privilege or disadvantage students? Cazden’s data showed teachers predominantly using a predictable three-part sequence in traditional lessons: teacher initiation, student response, and teacher evaluation (IRE). She also noted that in non-traditional lessons the IRE sequence was less prominent as students were granted more speaking rights, or less prominent depending on “the ways by which students get the right to talk—to be legitimate speakers—during teacher-led group activities” (Cazden, 2001, p. 82). By granting more speaking rights, “each student becomes a significant part of the official learning environment for all the others and teachers depend on students’ contributions to other students’ learning, both in discussions and for the diffusion of individual expertise through the class” (Cazden, 2001, p. 131). This is consistent with a complexity thinking view where contributions of individuals give rise to a collective body of knowledge. Herbel-Eisenmann & Cirillo (2009) reiterate this in their description of purposeful classroom discourse that develops through focused and determined efforts by students to build understanding with each other through their mathematical language use. In complexity thinking, meaningful exchanges fuel emergence. Meaningful exchanges are those communications that lead to transformation and the building of new insights or new ways of knowing that transcend the original body of knowledge (Olson & Eoyang, 2001). Conversely, behaviors that inhibit the sharing of knowledge block or interrupt emergence.
Substantial research on classroom discourse explores diverse ways in which students and teachers communicate, often focusing attention, in the mathematics classroom, on teacher-student talk, with emphasis on transmission models of teaching and cooperative approaches to participation and/or engagement in mathematics (Cobb et al., 1993; Forman & Ansell, 2001; Pimm, 1987). In contrast, Sfard (2007) broadened the definition of discourse to include “the different types of communication that bring some people together while excluding some others” (p. 573). Sfard also suggested a metaphor to highlight the importance of mathematical conversation in learning: thinking-as-communicating (Sfard & Kieran, 2001). By focusing on the social nature of the individual student, Sfard argued that learning mathematics means becoming fluent not only in the mathematical language or vocabulary but the broader and richer production of discourse. Sfard conceives of mathematical discourse as the use of four inter-related features, including mathematical word use, visual mediators, routines, and narratives. Learning, according to Sfard, is initiation into mathematical discourse and so requires an understanding of the mediating tools of interpersonal communication and the meta-discursive rules that shape and guide the general course of communicative activity.
Although research conducted in mathematics education through the lens of complexity (Doll, 1989; Kieren & Simmt, 2009; Reeder, 2005) provides data for describing the necessary minimum conditions, few researchers suggest practical ideas for teachers to use in creating conditions for emergence, and fewer still, provide analysis of students’ voices within a complex system. In mathematics, where thinking, or cognition, and communication necessarily go hand-in-hand, as Sfard’s (2008) neologism, “commognition,” implies it is vital that teachers find ways to stimulate meaningful communication and acquire tools to analyze the emerging discourse, so as to inform their pedagogy.
Research Context
Research Setting
I conducted this research within a community school set in a rural county of Nova Scotia, Canada. There were 10 boys and 13 girls in the Grade 6 class taught by one teacher with 14 years of experience at the elementary level. There were no visible minorities among these 23 students. Six students were receiving literacy support from a coach and two students were meeting with the itinerant teacher for mathematics support. The teacher described the overall achievement of the class in mathematics as average to low and generally stronger in the areas of literacy and social studies.
Goals of the Research Study
The primary goal of my research was to understand how and to what extent students participate autonomously in mathematical communication at the elementary level and to understand how student-centered mathematical discourse develops. Therefore, my goal differs from previous studies where the focus remained primarily on the role of the teacher and methodologies for teachers to try in order to promote, scaffold or develop discourse in the mathematics classroom (Chapman, 2009; Garrett, 2008; Nathan & Knuth, 2003).
As opposed to orchestrating a teaching experiment, I introduced the minimum conditions for complexity to increase autonomy, thereby creating an invitational space for student to explore independently their understandings of mathematical concepts and to participate collectively in the discourse of mathematics. Commensurate with a postmodern view of mathematics as tentative and embedded in human practices (Ernest, 1993), I was inspired by Owen’s (1997) comment for OST facilitators to “be prepared to be surprised” as opportunities for increased neighbor interactions and autonomy diminish teacher authority and encourage students’ mathematical knowledge to emerge in unconventional classroom conversations.
In my study, the teacher’s and researcher’s roles were to hold the space open (Owen, 1997) for student autonomy, allowing interactions and meaningful exchanges to flourish. Decentralized control of the space fostered accountability and responsibility in students who made self-directed choices to move (or not) through the space. In what follows, I describe the results of the students’ choices and analyze how the necessary minimum conditions for the complex learning system created possibilities for meaningful exchanges to occur.
The Research: Conversation Circle Topics
Sitting in one large circle, students were invited to propose topics for conversation. When a student offered a topic, they assumed the role of convener: to introduce the topic and to document the ensuing conversation. The following are examples of topics brought forth by the Grade 6 students:
Donnie: Patterns and Patterning in Times Tables,
Ethan: Word Problems,
Marcus: Strategies in Operations,
Claire: Art and Design in Mathematical Forms.
Students were given time to self-organize around topics of interest and meeting spaces. Relocated from their conventional Grade 6 classroom of desks and tables to open and fluid conversation circles, students freely moved about the room and quickly found ways to participate. As they considered which conversation circles to join, a cacophony of voices and chaotic movements followed. Corrigan’s (2002) notion of “freedom shock” aptly describes the students’ exuberant responses to such unprecedented amounts of choice and responsibility. Although OST provided a new and different format for the Grade 6 mathematics class, students reminisced about primary school storytelling circles. One student asked, “Are we supposed to feel like we are in Kindergarten again?” and another responded, “We can play telephone!” referring to the popular campfire game of whispering a message through a sequence of people that is typically played in a circle. This unusual setting in the mathematics classroom is nevertheless familiar to students and they quickly adjusted. Multiple audio and visual recordings stationed around the classroom captured the students’ experiences of OST and the details within each conversation circle. These recordings documented students’ movement and discourse, providing rich data for analysis.
Analysis
The data were analyzed iteratively with each pass focusing on one of the minimum conditions of complexity thinking necessary for emergence. I completed three iterations of analysis (see Table 1) to code the data. I documented the coding process to highlight the “language-in-use” (Gee, 2011) found in the data and then developed a discourse lexicon (see Appendix A) to assist teachers in the analysis of classroom discourse. The lexicon began with the first pass through the transcribed data to show instances of meaningful exchanges among students. Two subsequent passes through the data revealed themes and conversation threads among the conversation groups. I used these to organize the lexicon into emergent patterns found in the data. In its totality, the three iterations form an analytic lens for classroom discourse. For teacher researchers, using the tool connects complexity thinking theory and discourse analysis methods by making visible the dimensions of meaningful exchanges occurring (or not) in the classroom.
As per Table 1, in the first iteration of the analysis, I focused on the internal diversity, redundancy, and decentralized control of the learning system. I observed and documented the self-organization of students, namely, how they formed and reformed their physical groupings and how they chose to engage in conversation. Coding was used to unpack the nature of discourse and to show the extent to which the students participated in univocal (transmitting, receiving information) and dialogic (generating, listening, questioning) discourse (Knuth & Peressini, 2001). I built upon Truxaw and DeFranco’s (2008) model for mapping mathematics classroom discourse and conducted line-by-line coding of transcripts. Throughout the first iteration of the analysis, the coding of students’ physical grouping (whole class, small groups, dyads, individual) as well as the univocal and dialogic discourse structures in use made visible the extent to which control was decentralized and self-organization was present. Although students demonstrated significant capacity for self-organization, I also identified typical IRE (initiation, response, evaluation) patterns of interaction, including “teacher mimicry and illusory participation” (Truwax & DeFranco, 2008, p. 491). The IRE triad highlighted the occasional persistence of teacher mimicry, as an obstacle to authentic student self-organization.
In the second iteration, I focused on neighbor interactions to analyze the development of student discourse as ideas arose and moved around the room, within organized randomness (i.e., the balance of constraints on student activity and the freedom to move and engage). OST provides enough structure and choice to enable productive self-organization, hence the term liberating constraints (Davis et al., 2008). Organized randomness opens a space of opportunity in a learning system for discourse to develop through meaningful exchanges; however, the openness is not unbounded. The structure of OST (e.g., agenda topics, convener and note-taker, and rules of engagement) ensures some organization, while allowing for some autonomy (e.g., the choice to join and contribute to one’s preferred conversation circle and topic; the choice to move freely between conversation circles to ensure continuous learning or contribution; as well as, the choice to move outside of the circle formations and not participate). Stated somewhat differently, some structure contains student activity, without limiting discursive or creative possibilities. Teachers who work with the minimum conditions of complexity, such as organized randomness, may see a shift in student talk and classroom discourse as neighbor interactions bolster communication of mathematical understanding.
In the analysis of student discourse, I coded these possibilities as discourse functions (see Table 1), including initiating an opinion, giving information, elaborating, contextualizing, or evaluating ideas (Rymes, 2008; Setati & Barwell, 2006; Xu & Clarke, 2013). As part of this second iteration, I also coded mathematical discourse consistent with Sfard’s (2007) framework of word use, visual mediators, routines and narratives as students turned to problem solving, reviewing and representing their forms of mathematical knowledge. I included a full list of codes in the discourse lexicon (see Appendix A) to provide teachers with a range of students’ discursive moves for analysis. In addition, I created a discourse analysis table (see Appendix B) to further elaborate on each code used in the analysis. The discourse analysis table provides teachers with details about student dialogue and what to listen for as classroom discourse develops. I aligned these with examples from the data generated by the OST sessions to show the discursive moves associated within a specific discourse phase. These discourse phases became clearer to me as I moved through the third iteration of data analysis.
Table 1
Complexity Thinking Analytic Lens for Classroom Discourse
|
Complexity Thinking: Necessary Minimum Conditions |
Overall Discourse Focus |
Mathematics Classroom Discourse Focus: To What Extent do we See, Hear and/or Experience Student Talk |
|
|
First Iteration |
Internal diversity |
Participant's physical groupings/movement |
Whole class, small group, dyad, individual |
|
Redundancy |
Univocal—transmitting, receiving
Dialogic—generating, listening, questioning |
||
|
Decentralized control |
Discourse Structures |
Initiation, response, evaluation triad (including teacher mimicry and illusory participation) |
|
|
Second Iteration |
Organized Randomness |
Discourse Function |
Initiating an opinion, Giving information, Agreeing, Encouraging, Clarifying, Elaborating, Re-voicing, Contextualizing, Complementing, Conjecturing, Evaluating, Self-reflecting |
|
Neighbour Interactions |
Mathematical: 1.Sequence orienting 2.Forms of knowledge 3. Discourse use |
Mathematical: 1.Commenting, organizing, problem solving, reviewing 2.Procedures, concepts, strategies 3.Word use, visual mediators, routines, narratives |
|
My third iteration focused on identifying emergent patterns within the student discourse. One pattern, I named “Sharing.” This type of meaningful exchange represents offering an opinion or information; connecting with others through personal experience or stories; and accepting and encouraging others’ ideas. A second pattern, “Building,” signifies elaborating on or linking ideas to what others are saying. This type of meaningful exchange shows students orienting ideas through broader perspectives on issues, organizing thinking into greater coherence, and constructing or representing concepts through visual mediators. I termed a third meaningful exchange “Exploring.” This pattern includes evidence of students’ original and creative thinking (e.g., testing their ideas or make conjectures); expression of playfulness (e.g., entertaining new avenues of possibility, such as integrating poetry and mathematics, conveying a playful mindset in how they approach mathematics); and, articulation of “what-if”’ possibilities in their investigations (e.g., evaluating proposed arguments, applying learning or new learning in new contexts, self-reflecting on ideas).
OST conversations give students the latitude to play around with their topics, encouraging mathematics discourse. This self-organized “play” yields opportunities for students to orient themselves towards exploring ideas. Davis (1996) reminded teachers that, “Playing must be thought of as a sort of bricolage—an engaging in particular activities because one is able to do so, not because they are directed toward achieving any knowable ends. The function of playing is to open a space of possibilities” (p. 220). If students see the classroom as a space where play is possible and encouraged, then a different experience might await, replacing the expected work of the conventional mathematics class with joyful, unstructured activity leading to unknown possibilities and new knowledge.
During this iteration, I also noted student talk that could function as an obstacle to emergence and coded these as “Blocking,” which included telling more than listening, interrupting, controlling space, rejecting ideas and criticizing others. Blocking is often counterproductive to nurturing emergence, often preventing an idea from moving forward or creating a loss of focus so the idea is not fully developed and thereby compromising meaningful exchanges.
Self-organizing systems rely on meaningful exchanges to generate possibilities (emergence) that lead to a new order (convergence). The analytic tool of sharing, building, exploring and blocking, described above, provides the teacher researcher with a tool to understand more clearly the dynamics of meaningful exchanges. The discourse lexicon (see Appendix A) and discourse analysis table (see Appendix B) further clarify for teachers the types of meaningful exchanges found in the data with specific student dialogue examples. These examples parallel the coding used in each discourse phase as a means to support future classroom discourse analysis.
Meaningful Exchanges Using the Analytic Lens of Sharing, Building, and Exploring
Below are selected excerpts from conversations that took place with Grade 6 students participating in OST. I organize the descriptions according to the meaningful exchanges from the conversations. These excerpts are edited for readability and brevity. I omitted short segments of text for clarity; however, no words were changed from the transcripts. Teachers may recognize the sometimes disjointed feel of the students’ conversations. This, in part, may be due to the self-organizing principle of OST (Owen, 1997; Throop Robinson, 2018), and the opportunity for physical groupings of students to change even as the conversation continues. Every effort to identify students as they contributed to a conversation was made through the audio recordings. Visual recordings helped to confirm a student’s presence in a conversation circle and also recorded those students who were present but did not contribute verbally to the discussion.
I present an analysis of the selected transcript excerpts to illustrate how students use the discourse of mathematics to share, build and explore knowledge with each other. While other conversations remained significant in other ways, I chose to focus on these examples as they show more clearly the extent to which meaningful exchanges became visible within the learning system.
Sharing (e.g., Offering, Receiving, Connecting, Clarifying)
Students who chose to talk about “Patterns and Patterning in Times Tables” began their conversation with an initial sharing of what they thought the topic involved. The convener of the circle, Donnie, opened the conversation by initiating an opinion.
Table 2
Conversation About Patterns and Patterning in Times Tables: Introduction
|
Speaker |
Dialogue |
Type of Meaningful Exchange |
|
Donnie |
I think the patterns are the key things to the times tables because you’re just going up. |
Sharing (Initiating an opinion |
|
Ben |
I know. |
Sharing (Agreeing, Receiving an idea) |
|
Laura |
I think so |
Sharing (Receiving an idea) |
|
Katelyn |
Maybe. |
Sharing (Connecting with others’ ideas) |
|
Ben |
One times 38. |
Sharing (Giving an example) |
|
Donnie |
I think it is easier to use number patterns |
Sharing (Offering an opinion) |
|
|
[Overlapping voices] |
|
|
Katelyn |
Ok Donnie, make up something else |
Building (Encouraging others to build ideas) |
|
|
[Inaudible] |
|
|
Donnie |
So, in general what could patterns be used for? |
Sharing (Encouraging others to share) |
|
Ben |
Patterns could be used for everything. |
Building (Linking ideas) |
|
Donnie |
I know. When you think of it, it could be used for … anything. |
Sharing (Accepting others ideas) |
|
Katelyn |
They could be used to help you with math. |
Building (Re-voicing) |
Note. What is significant to note in this introduction to a conversation are the students’ efforts to generate ideas and accept the ideas on offer. Sharing of opinions and examples, prompting of further sharing and re-voicing of shared knowledge, set the stage for more meaningful exchanges.
The group continued to share ideas about patterns back and forth in this way, prompted again by the convener Donnie.
Table 3
Conversation About Patterns and Patterning in Times Tables: Development
|
Speaker |
Dialogue |
Type of Meaningful Exchange |
|
Laura |
I think that patterns are like this. |
Sharing (Clarifying ideas), Building (Representing through visual mediators) |
|
Ben |
Patterns … all you need to do is find it. |
Sharing (Offering an opinion) |
|
Katelyn |
Maybe patterns are used to help you. |
Sharing (Offering an opinion) |
|
Laura |
Yeah. |
Sharing (Agreeing) |
|
Donnie |
I think that they are. |
Sharing (Offering an opinion) |
|
Ben |
You just have to add the number that you want. |
Sharing (Contributing mathematical routine) |
|
Laura |
Times ten. |
Sharing (Giving an example) |
|
Donnie |
I think that patterns are… |
Sharing (Offering an opinion) |
|
Ben |
Times tables. |
Building (Elaborating on ideas) |
Note. Sharing an opinion took centre stage in the conversation as students engaged with the topic by making meaningful connections for each other.
Ben generalized the mathematical routine as Laura offered her visual mediator (see Table 6) as an example of patterning in the 10 times table.
Table 5
Laura’s Visual Mediator
|
1 |
X 10 |
10 |
|
2 |
X 10 |
20 |
|
3 |
X 10 |
30 |
|
4 |
X 10 |
40 |
|
5 |
X 10 |
50 |
Further evidence of sharing occurs through story fragments as students began to offer ideas about patterns that connected with prior experiences. For example, a little later on in this group’s conversation, Donnie invited others to share experiences on the topic.
Table 6
Conversation About Patterns and Patterning in Times Tables: Sharing Experiences
|
Speaker |
Dialogue |
|
Donnie: |
How about each of us tell a story about something that happened to them when they had to use patterns? Let’s tell a story when each of us had to use patterns. |
|
Ben: |
I use patterns all the time… |
|
Laura: |
You never know where… |
|
Ben: |
…like on games there are patterns. |
|
Donnie |
Like on video games. |
|
Laura |
Yeah. |
|
Donnie |
I use patterns going up to Halifax. |
|
Laura |
You see them every day. |
|
Donnie |
Like from the car. |
Note. The students’ offerings became more personal as students began sharing stories about using patterns outside the school and in a variety of contexts. Full transcripts of the conversation document Donnie’s story about playing video games where he constantly recognizes patterns and during his car trip to the city. Willingness to relate personal experiences among peers in this way indicates the comfort that students feel with each other.
These exchanges are meaningful for a number of reasons. First, there is clear evidence of students sharing in conversation as they make connections to personal life experiences and use mathematical words to offer examples about the topic that are meaningful to them. Their examples show understanding of mathematical concepts as students use patterning narratives to describe their use and relate them to familiar routines in multiplication tables. Secondly, the engagement in the topic is clearly felt with each contribution that the students share. The students’ input drives the conversation forward as each comment is accepted, inspiring others to make additional connections and share from their own perspective. Thirdly, students use the device of story fragments and the term “story” to motivate the conversation. These students predominantly chose to stay with this conversation circle throughout the math class, demonstrating engagement by their comments and questions.
Building (e.g., Elaborating, Linking, Re-voicing, Organizing, Reasoning)
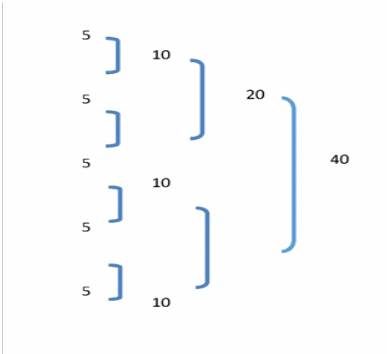
In the “Patterns and Patterning in Times Tables” conversation, the student talk shifted from sharing facts about patterns to building knowledge. Ben, working independently at first, drew a mathematical strategy to show others how he used a pattern to find solutions in multiplication (see Figure 1). In general, students did not make use of visual mediators in their mathematics discourse; however, Ben’s example proved to be meaningful for his group, as many of those students recorded similar visual mediators in their journals.
Figure 1
How Students Take up Patterning in Multiplication

Note.
This sequence shows how students
take up Ben’s doubling patterning in multiplication to
represent and construct their mathematical strategy piece by piece.
Table 7
Conversation About Patterns and Patterning in Times Tables: Efforts to Clarify Mathematical Thinking
|
Speaker |
Dialogue |
Type of Meaningful Exchange |
|
Katelyn: |
Ok wait, so what’s our numbers? |
Building (Organizing thinking) |
|
Ben: |
Put 8 fives down and look at the pattern... |
Building (Reasoning in mathematical context) |
|
[unknown]: |
Times table. |
Building (Contextualizing) |
|
Ben |
…and then you do the same thing with that… so, 20. Isn’t that cool? |
Building (Constructing mathematical concepts |
|
Katelyn |
Hanna, look at this … put 8 fives down … and then put … put that bar and what it equals. |
Building (Representing through visual mediators) |
|
Hanna |
5, 10. |
Building (Elaborating on ideas) |
|
Katelyn |
Yeah. Just put that bar and what it equals. |
Building (Linking ideas) |
|
Hanna |
10 |
Building (Elaborating on ideas) |
|
Katelyn |
Then you put two bars together for 10… equals 20 and then each equals 40. |
Building (Reasoning in mathematical context) |
|
Hanna |
What do you mean like? |
Sharing (Clarifying ideas) |
|
Hanna |
Ohhhh…. |
Sharing (Connecting with others’ ideas) |
|
Katelyn |
Works out really cool. |
Building (Complementing ideas) |
Note. Taken together, Ben’s introduction of the doubling strategy and his visual representation of the problem in his journal, along with Katelyn’s remodeling of the instructions and the problem for Hanna, indicate efforts in this circle group to clarify their mathematical thinking via verbal and visual information and to build upon their mathematical knowledge with each other.
After the above discussion, Ethan joined the group. Ethan took responsibility for his own learning by choosing to leave his original group and join the patterning conversation. Ben welcomed Ethan, specified the immediate subject of conversation, and then proceeded to revisit the patterning strategy with him from the beginning. Ben confidently rebuilt the question for Ethan by retelling the patterning sequence and representing it visually on paper while Ethan elaborated on the pattern with his own problem: 12 x 12.
The relocation of mathematics to circle conversations, combined with movement between the conversations, helped students construct knowledge. Firstly, this cross-pollination of ideas through neighbor interactions built a new series of problems for this group to solve, based on Ben’s doubling strategy. Secondly, a willingness to welcome new arrivals provided opportunity for the group to take more ownership of their math work. Explanations to the newcomer from various members were fluid and supportive, as they organized and demonstrated Ben’s strategy. As a result, Ethan’s role as a newcomer to this conversation circle helped solidify and spread the learning.
Other examples of building are seen in the “Art and Design in Mathematical Forms” conversation. Claire, the convener, suggested a challenging task. In doing so, she set the stage for her peers to work toward building on one another’s ideas in the session. Immediately following the group’s formation, she asked those present to create poems about mathematics collaboratively (see Table 8).
Table 8
Conversation About Art and Design in Mathematical Forms: A Collaborative Mathematical Challenge
|
Speaker |
Dialogue |
Type of Meaningful Exchange |
|
Claire: |
Ok. There was this game that I saw on the Internet a while ago … what you do is you take one starting word and then you go around in a circle and everyone will write the first thing that comes to their mind when they read the word that was written down above theirs and then you write it down and then you pass it to someone else and then, say if we started with the word eyeball, and then someone said blue, and then the next person said clouds, and the next person said sky and if the next person thought that the first thing that came to their mind from sky was water and it would start a whole new different topic. |
Building (Encouraging others to build on ideas) |
|
Overlap: |
Oh, cool. |
Sharing (Agreeing) |
Note. Claire’s willingness to share her experience puts an idea in the space for consideration and also signals her desire to move the group in a particular direction with a specific idea. Claire’s collaborative mathematical challenge is unlike anything the students have come to know as “doing mathematics.” Her activity invited engagement with a mathematics topic through language with the aim of creating a concrete outcome (a poem).
Claire’s task challenged students to build on each other’s ideas as they created the poem—a collaborative practice. It also simultaneously shifted their language use into a mathematical context, thereby establishing a link between numeracy and literacy learning. With Claire’s insistence that their poem begin with a mathematics word, Hanna offered the first word to initiate the collaborative process. Claire guided the process and transcribed as the other students built the new mathematics poem:
Table 9
Conversation About Art and Design in Mathematical Forms: Linking Ideas and Organizing Thinking in a Meaningful Way
|
Speaker |
Dialogue |
Type of Meaningful Exchange |
|
Claire |
What word should we start with next? |
Sharing (Encouraging others to share) |
|
Anna |
Pizza. |
Sharing (Giving an example) |
|
Claire |
No, we should start with a math word. |
Building (Orienting through broader perspective) |
|
Hanna |
Like dividing. |
Building (Contextualizing) |
|
Claire |
First word that comes to mind. |
Building (Encouraging others to build on ideas) |
|
Amanda |
Adding. |
Sharing (Giving an idea) |
|
Emma |
Subtracting. |
Building (Complementing ideas) |
|
Hanna |
What are you putting down? |
Sharing (Clarifying ideas) |
|
Claire |
Plus sign. |
Building (Complementing ideas) |
|
Amanda |
For adding. |
Building (Linking ideas) |
|
Claire |
Numbers plus sign. |
Building (Complementing ideas) |
|
Hanna |
You should put adding. |
Sharing (Offering an opinion) |
|
Claire |
What? |
Sharing (Encouraging others to share) |
|
Chantal |
Red Cross. |
Building (Complementing ideas) |
|
Anna |
Favorite numbers. |
Sharing (Offering an opinion) |
|
Claire |
Cool. |
Sharing (Agreeing) |
|
Hanna |
Can I read them? |
Building (Organizing thinking) |
|
Claire |
Sure. |
Sharing (Agreeing) |
|
Hanna |
Division, math, numbers, adding, plus sign, red cross, favorite numbers. |
Building (Re-voicing) |
Note. Sharing continued at this conversation circle in a variety of ways: eliciting ideas, offering opinions, and clarifying comments. Additionally, students began to run with Claire’s proposal and began elaborating on it by building mathematical context around the word play. Students added on to each other’s ideas by linking ideas and organizing thinking in a meaningful way as Hanna demonstrated in her final re-voicing of the group’s ideas. Of note is the initial stance that Claire assumed as the convener of this conversation. Initiating a new task prompted the students to share ideas and her generative comments encouraged them to build a math poem together, largely without directing the sequence. Through building, these meaningful exchanges represent genuine collaboration.
In this sequence, Claire and her peers had decided to “do mathematics” in a very different way. Claire’s integration relocated mathematical thinking in the minds of her peers from a stand-alone subject area to one that encompasses at least one other subject area by building on the literacy model and opens the door to link mathematics potentially with other disciplines across the curriculum. Claire’s topic indicates a belief about mathematics’ broad applicability, with the potential to explore links across subject areas. Even Claire’s title for the group, “Art and Design in Mathematical Form,” expresses her topic in a way that promoted subject integration with her peers, opening the subject up to greater possibilities than students would normally anticipate in a mathematics classroom.
The self-organization of OST allows for thought-provoking and perhaps unconventional topics, which in turn gives others an opportunity to participate in unexpected topics. Traditional spaces would make such student suggestions more difficult to surface. Or, teachers might evaluate what is a good idea or task and what is not, thereby potentially block or dismiss students’ interests. The freedom for students to create their own conversations allows for sometimes surprising results and often leads to unexpected creative outputs.
Exploring (e.g., Expressing Playful Mindset, Testing Ideas, Evaluating, Self-Reflecting)
Students’ enthusiasm and sense of play at the beginning of the “Patterns and Patterning in Times Tables” conversation demonstrates a mindset conducive to exploration. Students expressed the notion that they might have some fun while doing math. This comment indicates a student’s sense of curiosity and play in exploring mathematical ideas. While working to find patterns in the times tables, the convener offhandedly made a comment that leads to play (see Table 10).
Table 10
Conversation About Patterns and Patterning in Times Tables: Playing With Patterns
|
Speaker |
Dialogue |
Type of Meaningful Exchange |
|
Donni |
Sometimes you just do it for fun. |
Exploring (Expressing playful mindset) |
|
Ben |
I know. Sometimes you just want to have some fun. |
Exploring (Expressing a playful mindset) |
|
Marcus |
I think that this group is really cool. |
Sharing (Making observations) |
|
Anna |
Because Jason’s group is talking about wrestling. |
Sharing (Offering an opinion |
|
Ben |
You need patterns to make the tables. |
Exploring (Conjecturing about possibilities) |
|
Marcus |
I’m going to go walk around, okay? |
Sharing (Giving information) |
|
Donnie |
Okay. |
Sharing (Agreeing) |
|
Ben |
Okay, I’ll read what I wrote. |
Sharing (Giving an example) |
Note. The mindset expressed led the students to play around with patterns in multiplication, creating potentially new possibilities for knowledge building. Marcus, a visitor to the group, listened to the conversation from outside the circle and offered positive feedback. (“This group is cool”). Such encouragement helped to sustain exploration.
In the following segment, the teacher overheard the conversation and offered her own observation and additional words of encouragement. She did not alter the course of the conversation but simply helped sustain it, allowing the group to move from Ben’s earlier demonstration of a doubling pattern in the times tables to exploring the strategy further (See Table 11).
Table 11
Conversation About Patterns and Patterning in Times Tables: Building Understanding Through Reasoning Together and Testing Out Possibilities
|
Speaker |
Dialogue |
Type of Meaningful Exchange |
|
Laura |
Let’s find out a different pattern because this is really cool like… |
Exploring (Playing with ideas) |
|
Donnie |
Uh… how about nine? |
Exploring (Testing ideas) |
|
Laura |
Nine? |
Sharing (Receiving an idea) |
|
Ms. Stuart |
There is definitely a pattern in nine’s. |
Exploring (Evaluating proposed arguments) |
|
Katelyn |
We had eight fives and then we doubled them and that equals…. |
Building (Constructing mathematical concepts) |
|
Laura |
10 … and then 20 … double again and that equals 40. |
Building (Elaborating on ideas) |
|
Ms. Stuart |
That’s awesome. |
Sharing (Offering an opinion) |
|
Katelyn |
We made it really easy. |
Exploring (Evaluating proposed arguments) |
|
Donnie |
How many nines do we have? |
Sharing (Encouraging others to share) |
|
Ben |
It’s got to be an even number of nine’s or it won’t work. |
Exploring (Conjecturing about possibilities) |
|
Katelyn |
Huh? |
Sharing (Clarifying ideas) |
|
Donnie |
An even number? Ok so, how many are we going to have? |
Exploring (Encouraging others to explore ideas) |
|
Katelyn |
Eighteen … no, nine. |
Building (Elaborating on ideas) |
|
Laura |
Eight… eight…eight |
Building (Organizing thinking) |
|
Donnie |
No, nine. |
Sharing (Clarifying ideas) |
|
Ben |
You got to have an even number. |
Building (Orienting through broader perspectives) |
|
Donnie |
So the next one is even. |
Exploring (Conjecturing about possibilities) |
|
Ben |
What’s 18 and 18? |
Exploring (Applying knowledge) |
|
Building (Representing through visual mediator) |
|
|
Note. This longer sequence follows students as they build their understanding through reasoning together and begin testing out possibilities. For students, elaborating on ideas, added on to their understanding of mathematical procedures and strengthens mathematical concepts. Ultimately, this opened a space for play and conjecturing in the conversation as Ben’s observation about selecting an even number of digits indicates. Donnie picked this up and played with the idea through a visual mediator to document the conjecture and to show his reasoning.
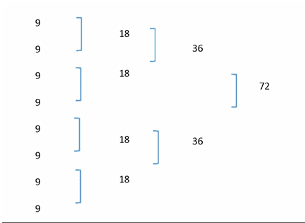
In this way, Ben’s insistence on having an even number of numbers in order for his doubling strategy to work provided an occasion for the group to delve into unknown territory and explore new possibilities in the realm of number theory. Asking questions such as, “What would happen if you multiplied an even number of odd numbers (e.g., 3 × 3 × 3 × 3) or an even number of even numbers (e.g., 2 × 2 × 2 × 2)?” or, “What would happen if you multiplied an odd number of odd numbers (e.g., 3 × 3 × 3) or an odd number of even numbers (e.g., 2 × 2 × 2)?” opened the door to a wider conversation that integrated patterning concepts naturally with multiplication concepts. Students began to consider these patterns from the level of multiplicative thinking rather than relying solely on earlier conceptions of multiplication as repeated addition or, perhaps, memorization of facts. A systematic investigation of such issues in number theory allows students to consider what makes sense in any given situation, to deepen their understanding of number relationships and so develop a broader sense of numeracy and confidence in problem solving. Ben and Donnie did exactly this in their exploration of pattern (See Figure 2).
Figure 2
Ben and Donnie’s Visual Mediator
To
understand more fully the dynamics of fun, creative energy, and
exploration, an excerpt from the “Strategies in Operations”
conversation reveals how a new voice can infuse the group with new
energy, influence a new exploration, and generate a more fun-filled
and engaging experience for all, including those who are resistant to
doing more work. As the “Addition Strategies” circle
began to explore their topic, Chantal opened up the context for
problem solving strategically (See Table 12).
Table 12
Conversation About Strategies in Operations: Opening Space for Different Strategies
|
Speaker |
Dialogue |
Type of Meaningful Exchange |
|
Chantal |
Can we use different strategies? |
Exploring (Conjecturing about possibilities) |
|
Anna |
What’s your other strategy? |
Sharing (Encouraging others to share ideas) |
|
Donnie |
Yeah, let’s try to make up one. |
Building (Encouraging others to build on ideas) |
|
Chantal |
We can all think of one. |
Building (Complementing ideas) |
|
Donnie |
I think if everybody made up a strategy and then we did them. |
Exploring (Conjecturing about possibilities) |
|
Kelly |
What? |
Sharing (Clarifying ideas) |
|
Donnie |
And then each other does their own strategy. |
Exploring (Expressing playful mindset) |
|
Chantal |
Tell Ms. Stuart. |
Building (Orienting through broader perspectives) |
|
Marcus |
I know one. I love your group; it’s fun. |
Sharing (Offering an opinion) Exploring (Expressing playful mindset) |
|
Kelly |
Next time, I’m going to make a group. |
Exploring (Self-reflecting on ideas) |
|
Chantal |
I wish I was a group leader. |
Sharing (Offering an opinion) |
|
Kelly |
So do I. |
Sharing (Agreeing) |
Note. Generating ideas led to a sense of playfulness as Chantal began to open the space wider to accept different ways to solve problems and to explore possibilities for creating unique strategies. Sharing and building are evident in students’ clarifying and questioning moves while conjecturing becomes the impetus to move the group’s conversation forward into uncharted territory without direct consultation from the teacher.
Anna, Donnie, and Chantal all encouraged the group to explore and invent other strategies to push the group’s thinking further. Donnie’s proposal demonstrates the power of minimal conditions to generate participant accountability for learning, rendering teacher authority unnecessary. Even when Chantal requested that the group inform the teacher about their new change in direction, no one picked up on her request. The group had established its autonomy and accountability. The group had created momentum and this energy attracted Marcus who described it as “fun.” Coming together to explore a topic, generated meaningful exchanges, energizing and uplifting the group in the process.
Blocking (e.g., Telling More Than Listening, Interrupting, Controlling, Rejecting Ideas, Criticizing)
At times, student offerings in conversations are met with significant blocking (Baines, Rubie-Davies, & Blatchford, 2009) from peers, despite students’ efforts to engage or contribute to meaningful exchanges. To ensure the viability of the learning system, students must be free to seek other conversations. This ability to self-organize is the lifeblood of the complex learning system. The aim is to provide just enough structure to guide students (shared purpose, basic rules of engagement) while maximizing autonomy to increase the probability of meaningful exchanges. Too little structure and chaos may ensue; too much and connectivity, creativity and possibility are compromised. The condition of self-organization allows students to freely choose where and how they will contribute. Met with others’ efforts to block or inhibit contributions, as in the next excerpt, students are free to move to other conversations and away from the blocking to seek opportunities for meaningful exchanges.
Table 13
Blocking or Inhibiting Contributions
|
Speaker |
Dialogue |
Type of Meaningful Exchange |
|
Sarah |
Now it’s only Marcus, Jerome, Laura and me. |
Sharing (Giving information) |
|
Laura |
We need help. |
Sharing (Offering an opinion) |
|
… |
[inaudible] |
|
|
Marcus |
…trying to kill us all. Help us. Help us. |
Sharing (Offering an opinion) |
|
Jerome |
She’s not smart. |
Blocking (Criticizing others) |
|
Sarah |
What’s … divided by … ? |
Sharing (Encouraging others to share) |
|
Jerome |
You don’t even know that answer. |
Blocking (Rejecting ideas) |
|
Laura |
Maybe we should try. I don't know unless I try it. |
Exploring (Conjecturing about possibilities) |
|
Jerome |
Even if you tried you wouldn’t know. |
Blocking (Interrupting, Telling more than listening) |
|
Sarah: |
You take away 2 … how many do you have? |
Sharing (Encouraging others to share) |
|
Laura |
Go do something else if you don’t like it. |
Blocking (Controlling space) |
Note. Jerome’s first block is a direct put down of one of the group members. Jerome positioned Sarah as “non-mathematician” perhaps in an attempt to build his own identity in the eyes of his peers. Increasingly, he subordinated her thinking to his own with a second and third block, thereby impeding the progress of the conversation. Rejecting an idea may only temporarily block a student from engaging in the conversation; however, blocking a speaker and controlling the space of the conversation verbally by talking over her or him will undoubtedly lead to complete shutdown. Admirably, Sarah refused to let him close the space for her; and, as Laura challenged the block by asserting herself within the space, the two students returned to their problem. However, Jerome’s behavior caused distraction and inhibited collaboration from the other students.
When students block it makes it more difficult for others to learn or contribute as the block functions as an obstacle to progress and inhibits or slows down meaningful exchanges.
Summary
The format of OST provided the conditions (i.e. internal diversity, redundancy, decentralized control, organized randomness, neighbor interactions) needed to create a complex system. These conditions encouraged networks of students to interact in meaningful ways through sharing information around a common theme, playfully building knowledge, and harnessing creative energy to explore possibilities and thereby supporting dialogic classroom discourse. With these conditions met, students appeared more likely to participate and engage in meaningful exchanges. From these extracts it is noted that particular students participated in collaborative conversations sustained through mutual interests and the excitement of creative input from peers, while in other sequences, students chose to inhibit meaningful exchanges through blocking. Insights from this phenomenon together with the meaningful exchanges will be discussed further in the section that follows.
As stated earlier, I have included a Discourse Lexicon (see Appendix A), to show the discursive moves of those students who engaged in sharing, building and exploring as well as those choosing to block or shut down conversations. My intention in building the discourse lexicon is to support teachers in identifying discursive phases in their classroom. In Appendix B, I have included a Discourse Analysis Table to provide examples of students’ discursive moves together with sample student dialogue drawn from the data to show how each discourse phase was identified. The examples in the Tables above and in the Discourse Analysis Table were selected for clarity and are intended to be representative of the types of emerging classroom discourse rather than exhaustive. The Discourse Analysis Table may support teachers’ analysis with examples of what to listen for in their classroom, examples of student dialogue that can be used as exemplars for the discourse phases, and from these, insights into developing more meaningful discourse and effective communication among students.
Discussion
Internal Diversity, Redundancy and Decentralized Control: Sharing Through Storytelling
Although all of the five conditions for a complex learning system work together to create emergence and a new order, internal diversity, redundancy and decentralized control lay a critical foundation for the sharing pattern. Student demographics, personal experiences, and thinking styles need to be different enough, yet similar enough to create creative possibilities through sharing. And, the de-centralized control provides the opportunity to share their stories.
Students participated frequently in sharing story fragments with their peers throughout all the conversations. Necessary student diversity and redundancy sustained the system and ensured that new ideas and insights could emerge from sufficient commonalities to work towards similar goals. Adequate internal diversity existed among the students, given the range of preferences and learning styles documented by the teacher and shared with me in our pre-research conferences. Yet, enough redundancy, given the students’ similar schooling experiences with learning mathematics, ensured a cohesive impression of the working environment. Decentralized control became an essential pedagogical shift in my research with the teacher present in the classroom, along with the researcher, with neither leading the students during their conversations. Decentralized control provided significant autonomy to students who, typically, were accustomed to being told what to do and when to do at school. For the teacher this meant a significant “letting go” (Davis & Sumara, 2006) of the role of authority figure and director for these students, who rose to the responsibility in many ways.
In some cases, students’ appropriation of the IRE structure mimicked the teacher’s voice and control of the classroom discourse. In others, students entered a dialogic phase of discourse in their listening, questioning and ability to generate conversation among peers. Overall, a general relocating of familiar exchanges and practices from the conventional classroom (e.g., reading, writing, telling stories) occurred in the mathematics classroom. Asking students to converse within a space created by the minimum conditions for complexity offered students an opportunity to integrate previously introduced classroom practices in the mathematics classroom, as they shared and developed mathematical knowledge. As a result, a rich classroom discourse emerged as students drew upon prior knowledge to create these meaningful exchanges.
Sharing, initially, became the discernible pattern for their meaningful exchanges. As students participated in sharing as storytelling (perhaps a natural result of the circle formation) and commenting on others’ stories, they seamlessly and explicitly connected their understanding of mathematics to the wider world, thereby demonstrating meaningful exchanges. Students’ stories contributed to the development and use of mathematics discourse as they also enabled more use of mathematical words, narratives, and routines (Sfard, 2007), which they used to make conversations personally relevant and meaningful to others. This is seen in their exchanges about the prevalence of patterns in their world (i.e. “they’re everywhere”), the usefulness of patterns (i.e. in problem solving, multiplication, art and design), and the opportunities to create their own patterns (examples recorded in student journals).
Organized Randomness and Neighbor Interactions: Building Through Movement
The minimum conditions for a complex learning system moved the students from a hierarchically structured or conventional classroom to a self-organizing, open-space classroom full of movement, thereby increasing the opportunity for meaningful student interaction. Students were encouraged to leave or join circle conversations, using their level of engagement as a barometer to maintain a constant or as needed infusion of energy. As a result, there was generally considerable movement through the classroom space as students grouped and regrouped according to areas of interest, opportunities that arose, and changes to group dynamics. Physical movement was critical to transition to the sharing pattern, during which ideas are presented, to the building pattern, during which students add on to the ideas shared to move the ideas along and develop the discourse.
Claire convened her “Art and Design in Mathematical Forms” conversation with a clear purpose. Although task-oriented, she encouraged her peers to engage with new ideas and to build upon those ideas together, generating high energy and the fast-paced movement of fresh ideas. In contrast to conventional mathematical lessons, the task of collaboratively creating a poem, rather than independent practice of procedural skills, demonstrates the building pattern as students elaborated, linked, and constructed ideas resulting in a dynamic exchange. Her efforts to negotiate a task through sharing, (clarifying and accepting), laid the foundation for transitioning to this building pattern. Claire oriented the work of the mathematics classroom through a broader perspective in successfully combining notions of literacy with numeracy and moving the subject matter toward an inter-disciplinary approach. Through their use of words, narrative, and routine, Claire’s group participated in mathematics discourse to build and communicate knowledge together.
The temporary change to the mathematics classroom built networks among the students, increased students’ self-motivation, and fostered the movement of ideas and energy through the system, as students showed their accountability for learning by moving into and contributing to conversation circles of choice. Some students’ talk or neighbor interactions moved ideas through sharing to building upon what was shared and, as I will discuss next, to exploring possibilities.
Emergence: Exploring Through Creative Play
Using the OST methodology, the classroom research established the conditions needed to create a complex learning system. These conditions formed networks of students who interacted by sharing information around a common theme, by building on ideas, and by harnessing creative energy, exploring possibilities as knowledge emerged. These meaningful exchanges support a shift from univocal, teacher-directed discourse to more student-led, dialogic classroom discourse to establish new ways of thinking about mathematics. The data showed evidence of purposeful classroom discourse as students demonstrated their confidence in problem solving and reliance on other students for expertise and assistance. In addition, the students also exhibited playful, energetic dialogue as the sharing, building, exploring patterns emerged.
I identified exploring as students conjecturing, often playfully, about future possibilities, testing ideas to look beyond the familiar, evaluating proposed arguments, applying knowledge, and self-reflecting to see new pathways and mine insight. When exploration emerged as the students developed ideas by proposing new questions and strategies for activities, so did the playful, creative energy. In those sequences where exploration progressed, students also articulated the notion of having fun. This surprising realization overcame previous expressions in student interviews and journals of mathematics as hard work. The shift from doing work to having fun is significant. Students began to experience the work of the mathematics classroom not only as a series of questions to be answered but also as a creative exploration to be enjoyed, probed and interrogated. Challenging the conventional paradigm of classroom work becomes critical, as something other than work becomes productive, notably play and the playful fun of trying something new.
Integrating play in the mathematics classroom may move students to enact their understanding when interacting with others and engaging in imaginative creations (Conklin, 2014) that are at once playful, fun, and innovative. The relaxed atmosphere and sense of play evoked by sitting in a circle and offering self-organization connected these students to the openness of the space, which in turn facilitated an enriched mathematical discourse.
Self-organization also produced unexpected combinations of diverse students who could share, build, and explore a topic in interesting ways through their differences. Diversity, when embraced, is fuel for creative and purposeful play, through which new possibilities emerge. At this critical point, the learning system pays attention and begins to look for convergence, which occurs when what has emerged is then adopted by the system to create a new order, in this case, new mathematical understanding. This pattern of emergence and convergence arose in some circles where students demonstrated sustained engagement in mathematical discourse. For example, the introduction of Ben’s Doubling Strategy opened the way for Donnie to explore with his group members how this strategy might expand their understanding of more patterns in the times tables. Donnie’s infusion of energy and enthusiasm for Ben’s work caused further instances of sharing among the students and led some to play with additional possibilities in their journals. In Claire’s case, her creative energy imparted an alternative perspective on the idea of math work and engaged the group in conversation outside a strictly mathematical realm. Dialogic discourse emerged for these students in the back-and-forth statements of inquiry and clarification heard throughout the exchanges as well as in the beginning of exploring possibilities (e.g. “I want to test something,” or “This looks like fun”). Students offered their creative ideas or took up the ideas of others as a fun way to do mathematics and, in so doing, sustained their engagement with the conversations.
Conclusions
Creating Environments That Encourage Meaningful Exchanges
My research focus has been on the mathematics classroom and how complexity thinking might illuminate aspects of student participation and interaction previously invisible to me. I have seen that through the lens of complexity thinking students experience the “work” of the mathematics classroom differently as critical minimum conditions make room for new opportunities. Providing the minimum conditions through OST allowed for increased student interactions, and therefore, more purposeful classroom discourse. This led to three distinct types of meaningful exchanges in the elementary mathematics classroom: sharing (offering, receiving, clarifying), building (elaborating, organizing, reasoning), and exploring (expressing playful mindset, conjecturing, evaluating). As conversations developed, the momentum of the sharing, building and exploring patterns was occasionally interrupted with instances of blocking by students, causing meaningful exchanges to be compromised. Nevertheless, the emphasis on self-organization encouraged students to seek meaningful exchanges in other conversations.
While previous studies of classroom discourse tend to focus on, for example, the teacher’s perspective of learner-focused discourse (Chapman, 2009), teacher-to-student interaction (Chapin, O’Connor & Canavan-Anderson, 2003) and, in particular, ways for teachers to direct or “manage” discourse in order to “ensure” student participation and understanding (Kilpatrick & Swafford, 2002), my research highlights the result of student-to-student interactions in the context of the complex learning system. Such opportunity to immerse myself in complexity thinking research has offered new perspectives on teaching mathematics and on mathematics education in general.
Considerations for Classroom Research in Mathematics Education
My view of this research through the lens of complexity thinking meant considering the implications of the findings at each level of emergence, that is, for mathematics education, for classroom discourse analysis, and for research methodologies. Through the course of this research, I recognized that an intensive analysis of classroom discourse reveals insights otherwise lost in the bustle of a busy classroom. The development of the complexity thinking analytic lens for classroom discourse afforded me clearer perceptions through three iterations of the nature of classroom discourse and how students take up various discursive uses to share, build, and explore mathematical meaning together. For me, first as a classroom teacher and now as researcher, I appreciate these insights as they provide me with evidence to help re-imagine teachers’ practices and support on-going efforts to effect change with students. This discourse analysis has encouraged me to undertake future research opportunities with teachers who may find new understandings for their teaching and learning in the student discourse.
Many questions continue to arise for me as I consider the implications of the findings. For example, how to best support students in creating meaningful exchanges to build capacity for increased sharing, building, and exploring, and how to best assist students in the art of hosting a conversation. Could sharing, building, and exploring increase by investing in the development of communication skills for participants specifically? In my study, I did not focus on a teacher’s responsibility to orchestrate classroom discourse; rather, I highlighted the simple rules for classroom interaction to nurture more meaningful exchanges and intense conversations for students. Questions remain regarding the teacher and researcher’s role in holding the classroom space open so that discourse might unfold fruitfully for students. Throughout this study, efforts were made to empower students and stimulate engagement through freedom of expression and choice generated rich data. I remain open to future possibilities for classroom discourse analysis that is informed by complexity thinking and the minimum conditions to foster emergence in hopes of illuminating meaningful exchanges for students and teachers alike.
References
Baines, E., Rubie-Davies, C., & Blatchford, P. (2009). Improving pupil group work interaction and dialogue in primary classrooms: Results from a year-long intervention study. Cambridge Journal of Education, 39(1), 95–117. doi: 10.1080/03057640802701960
Barwell, R. (2005). Ambiguity in the mathematics classroom. Language and Education, 19(2), 118–126.
British Columbia (BC) Ministry of Education. (2019). Mathematics Curriculum. Victoria, BC: Government of British Columbia.
Burns, A., & Knox, J. S. (2011). Classrooms as complex adaptive systems: A relational model. The Electronic Journal for English as a Second Language, 15(1), 1–25.
Cazden, C. (2001). Classroom discourse: The language of teaching and learning, (2nd ed). Portsmouth, NH: Heinemann.
Chapin, S. H., O' Connor, C., & Canavan-Anderson, N. (2003). Classroom discussions: Using math talk to help students learn, Grades 1–6. Sausalito, CA: Math Solutions.
Chapman, O. (2009). Learner-focused discourse in learning mathematics: A teacher’s perspective. In S. L. Swars, D.W. Stinson, & S. Lemons-Smith (Eds.), Proceedings of the 31st annual meeting of the North American chapter of the international group for the psychology of mathematics education (pp. 328–336). Atlanta, GA: Georgia State University.
Cobb, P., Wood, T., & Yackel, E. (1993). Discourse, mathematical thinking, and classroom practice. In E. A. Forman, N. Minick, & C. A. Stone (Eds.), Contexts for learning: Sociocultural dynamics in children’s development (pp. 91–119). New York, NY: Oxford University Press.
Cobb, P., Wood, T., Yackel, E., & McNeal, B. (1992). Characteristics of classroom mathematics tradition: An interactional analysis. American Educational Research Journal, 29, 573–604.
Conklin, H. G. (2014). Toward more joyful learning: Integrating play into frameworks of middle grades teaching. American Educational Research Journal, September, 1–29.
Corrigan, C. (2002). Open space technology and the legacy of education. www.chriscorrigan.com
Davis, B. (1996). Teaching mathematics: Toward a sound alternative. New York, NY: Routledge.
Davis, B., & Simmt, E. (2003). Understanding learning systems: Mathematics education and complexity science. Journal for Research in Mathematics Education, 34(2), 137–167.
Davis, B., & Sumara, D. (2006). Complexity and education: Inquiries into learning, teaching, and research. Mahwah, NJ: Lawrence Erlbaum.
Davis, B., Sumara, D., & Luce-Kapler, R. (2008). Engaging minds: Changing teaching in complex times (2nd ed). New York, NY: Routledge.
Doll, W. E. Jr. (1989). Complexity in the classroom. Educational Leadership, 47(1), 65–70.
Doll, W. E. Jr. (1993). A post-modern perspective on curriculum (Vol. 9). New York, NY: Teachers College Press.
English, L. D. (2008). Introducing complex systems into the mathematics curriculum. Teaching Children Mathematics, 15(1), 38–47.
Ernest, P. (1993). Conversation as a metaphor for mathematics and learning. In Proceedings of British Society for Research into Learning Mathematics, 13(3), 58–63. Manchester, UK: Manchester University.
Forman, E., & Ansell, E. (2001). The multiple voices of a mathematics classroom community. Educational Studies in Mathematics, 46(1), 115–142.
Garrett, T. (2008). Student-centered and teacher-centered classroom management: A case study of three elementary teachers. Journal of Classroom Interaction, 43(1), 34–47.
Gee, J. P. (2011). How to do discourse analysis: A toolkit. New York, NY: Routledge.
Herbel-Eisenmann, B., & Cirillo, M. (Eds.). (2009). Promoting purposeful discourse: Teacher research in mathematics classrooms. Reston VA: NCTM.
Herbel-Eisenmann, B., & Otten, S. (2011). Mapping mathematics in classroom discourse. Journal for Research in Mathematics Education, 42(5), 451–485.
Johnson, S. (2001). Emergence: The connected lives of ants, brains, cities, and software. New York, NY: Scribner.
Kieren, T., & Simmt, E. (2009). Brought forth in bringing forth: The interactions and products of a collective learning system. Complicity: An International Journal of Complexity and Education, 6(2), 20–28.
Kilpatrick, J., & Swafford, J. (Eds.). (2002). Helping children learn mathematics. Washington, DC: National Academy Press.
Knuth, E., & Peressini, D. (2001). A theoretical framework for examining discourse in mathematics classrooms. Focus on Learning Problems in Mathematics, 23(2 & 3), 5–22.
Maas, F., & Maas, J. (2005). Principled interconnections: Complexity and classroom learning. Paper presented at the Complexity, Science and Society Conference, The University of Liverpool, UK, September 12, 2005.
Manouchehri, A. (2007). Inquiry-discourse mathematics instruction. Mathematics Teacher, 101, 290–300.
Miranda, H., Beisigel, M., Simmt, E., Davis, B., & Sumara. D.. (2006). Consciousness, collectivity and culture: Experiences of intimacy in mathematics learning. Journal of the Canadian Association for Curriculum Studies, 4(2), 123–137.
Nathan, M. J., & Knuth, E. J. (2003). A study of whole classroom mathematical discourse and teacher change. Cognition and Instruction, 21(2), 175–207.
National Council of Teachers of Mathematics (NCTM). (2014). Principles to Actions: Ensuring Mathematical Success for All. Reston, VA: NCTM.
Newell, C. (2008). The class as a learning entity (complex adaptive system): An idea from complexity science and educational research. SFU Educational Review, 2(1), 5–17.
Nova Scotia Department of Education and Early Childhood Development (NSDEECD). (2014). Mathematics Curriculum. Halifax, NS: Nova Scotia Government.
Olson, E., & Eoyang, G. (2001). Facilitating organization change: Lessons from complexity science. San Francisco: John Wiley & Sons.
Osberg, D., & Biesta, G. (2007). Rethinking schools through the ‘logic’ of emergence: Some thoughts on planned enculturation and educational responsibility. In J. Bogg & R. Geyer (Eds.), Complexity science and society (pp. 35–38), Oxford, UK: Radcliffe.
Owen, H. (1997). Open space technology: A user’s guide, (2nd ed). San Francisco, CA: Berrett-Koehler.
Pimm, D. (1987). Speaking mathematically: Communication in mathematics classrooms. London, UK: Routledge.
Reeder, S. (2005). Classroom dynamics and emergent curriculum. In W. E. Doll Jr., M. J. Fleener, D. Trueit, & J. St. Julien. (Eds,). Chaos, complexity, curriculum, and culture: A conversation (pp. 247-260). New York, NY: Peter Lang.
Rymes, B. (2008). Classroom discourse analysis: A tool for critical reflection. Cresskill, NJ: Hampton Press.
Sawada, D., & Caley, M. (1985). Dissipative structures: New metaphors for becoming in education. Educational Researcher, 14(3), 13–19.
Setati, M., & Barwell, R. (2006). Discursive practices in two multilingual mathematics classrooms: An international comparison. African Journal for Research in Mathematics, Science and Technology Education, 10(2), 27–38.
Sfard, A. (2007). When the rules of discourse change, but nobody tells you: Making sense of mathematics learning from a commognitive standpoint. The Journal of the Learning Sciences, 16(4), 567–615.
Sfard, A. (2008). Thinking as communicating: Human development, the growth of discourses, and mathematizing. New York, NY: Cambridge University Press.
Sfard, A., & Kieran, C. (2001). Cognition as communication: Rethinking learning by talking through multi-faceted analysis of students’ mathematical interactions. Mind, Culture, and Activity, 8(1), 42–76.
Throop Robinson, E. (2016). Open Space Technology: Complexity thinking, classroom discourse, and mathematics learning in the elementary classroom, (Unpublished doctoral dissertation). National Library of Australia, https://trove.nla.gov.au/version/242328980
Throop Robinson, E. (2018). Mapping complexity in an elementary mathematics classroom. Canadian Journal of Action Research, 19(3), 5–33. doi: 10.33524/cjar.v19i3.423
Truxaw, M. P., & DeFranco, T. (2008). Mapping mathematics classroom discourse and its implications for models of teaching. Journal for Research in Mathematics Education, 39(5), 489–525.
Urry, J. (2005). The complexity turn. Theory, Culture, and Society, 22(5), 1–14. doi: 10.1177/0263276405057188
Wheatley, M. J., & Frieze, D. (2007). Beyond networking: How large-scale change really happens. The School Administrator, 64(4), 35–38. deborahfrieze.com/wp-content/uploads/2011/03/FriezeWheatley__Schooladmin.pdf
Willick, F. (2014, June 20). Nova Scotia School System Suffering from Mathophobia. The Chronicle Herald. http://thechronicleherald.ca/novascotia/1217075nova scotia-school-system-suffering-frommathophobia
Western and Northern Canadian Protocol (WNCP). (2006). The Common Curriculum Framework for K–9 Mathematics. Edmonton, AB: Government of Alberta.
Xu, L., & Clarke, D. (2013). Meta-rules of discursive practice in mathematics classrooms from Seoul, Shanghai and Tokyo. ZDM, 45(1), 61–72.